ЬтФПФкШн
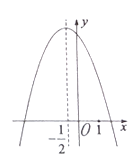
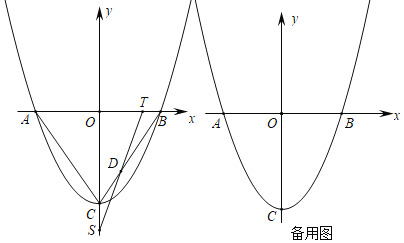
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуOЃЈ0ЃЌ0ЃЉЃЌAЃЈЃ5ЃЌ0ЃЉЃЌBЃЈ2ЃЌ1ЃЉЃЌХзЮяЯпlЃКyЃНЃЃЈxЃhЃЉ2ЃЋ1ЃЈhЮЊГЃЪ§ЃЉгыyжсЕФНЛЕуЮЊCЃЎ

ЃЈ1ЃЉlОЙ§ЕуBЃЌЧѓЫќЕФНтЮіЪНЃЌВЂаДГіДЫЪБlЕФЖдГЦжсМАЖЅЕузјБъЃК
ЃЈ2ЃЉЩшЕуCЕФзнзјБъЮЊycЃЌЧѓycЕФзюДѓжЕЃЌДЫЪБlЩЯгаСНЕуЃЈx1ЃЌy1ЃЉЃЌЃЈx2ЃЌy2ЃЉЃЌЦфжаx1ЃОx2Ён0ЃЌБШНЯy1гыy1ЕФДѓаЁЃЛ
ЃЈ3ЃЉЕБЯпЖЮOAБЛlжЛЗжЮЊСНВПЗжЃЌЧветСНВПЗжЕФБШЪЧ1ЃК4ЪБЃЌЧѓhЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЖдГЦжсxЃН2ЃЌЖЅЕуBЃЈ2ЃЌlЃЉЃЛЃЈ2ЃЉy1ЃМy1ЃЛЃЈ3ЃЉhЃН0ЛђhЃНЃ5ЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉНЋЕуBДњШыХзЮяЯпЕФНтЮіЪНЃЌЕУНтЮіЪНЃЌДгЖјЕУЕНХзЮяЯпЕФЖдГЦжсМАЖЅЕузјБъЃЛ
ЃЈ2ЃЉгУКЌhЕФЪНзгБэЪОyCЃЌдкИљОнЪНзгЬиЕуЧѓГіyCЕФзюДѓжЕМАДЫЪБЕФhжЕЃЌДЫЪБдйХаЖЯlдкxЃО0ЪБЕФдіМѕад;
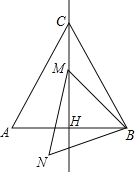
ЃЈ3ЃЉЩшlгыxжсЕФНЛЕуЮЊMЃЌдђOM=ЃЈ1/5ЃЉOAЛђAM=ЃЈ1/5ЃЉOAЃЌНјЖјЕУЕНMЕФзјБъЃЌДњШыНтЮіЪНЃЌЧѓЕУhЕФжЕЃЎ
ЪдЬтНтЮіЃК
НтЃКЃЈlЃЉАбxЃН2ЃЌyЃН1ДњШыyЃНЃЃЈxЃhЃЉ2ЃЋ1ЃЌЕУhЃН2ЃЎ
ЁрНтЮіЪНЮЊyЃНЃЃЈxЃ2ЃЉ2ЃЋ1ЃЈЛђyЃНЃx2ЃЋ4xЃ3ЃЉЃЎ
ЖдГЦжсxЃН2ЃЌЖЅЕуBЃЈ2ЃЌlЃЉЃЎ
ЃЈ2ЃЉЕуCЕФКсзјБъЮЊ0ЃЌдђyCЃНЃh2ЃЋ1ЃЌ
ЁрЕБhЃН0ЪБЃЌyCгазюДѓжЕЮЊ1ЃЎ
ДЫЪБЃЌlЮЊyЃНЃx2ЃЋ1ЃЌЖдГЦжсЮЊyжсЃЌЕБxЁн0ЪБЃЌyЫцзХxЕФдіДѓЖјМѕаЁЃЎ
Ёрx1ЃОx2Ён0ЪБЃЌy1ЃМy1ЃЎ
ЃЈ3ЃЉАбOAЗж1ЃК4СНВПЗжЕФЕуЮЊЃЈЃ1ЃЌ0ЃЉЛђЃЈЃ4ЃЎ0ЃЉЃЎ
ЂйxЃН-1ЃЌyЃН0ДњШыyЃНЃЃЈxЃhЃЉ2ЃЋ1ЃЌЕУhЃН0ЛђhЃНЃ2ЃЎ
ЕЋhЃНЃ2ЪБЃЌOAБЛЗжЮЊШ§ВПЗжЃЌВЛКЯЬтвтЃЌЩсШЅЃЎ
ЂкЭЌбљЃЌАбxЃНЃ4ЃЌyЃН0ДњШыyЃНЃЃЈxЃhЃЉ2ЃЋ1ЃЌЕУhЃНЃ5ЛђhЃНЃ3ЃЈЩсШЅЃЉ
ЁрhЃН0ЛђhЃНЃ5ЃЎ

 МЄЛюЫМЮЌгХМгПЮЬУЯЕСаД№АИ
МЄЛюЫМЮЌгХМгПЮЬУЯЕСаД№АИ ЛюСІЪдОэЯЕСаД№АИ
ЛюСІЪдОэЯЕСаД№АИ ПЮПЮгХФмСІХргХ100ЗжЯЕСаД№АИ
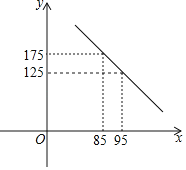
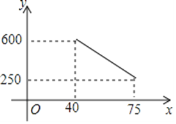
ПЮПЮгХФмСІХргХ100ЗжЯЕСаД№АИЁОЬтФПЁПЮфККЁАаТЙкЗЮбзЁБЗЂЩњвдРДЃЌФГвНСЦЙЋЫОЛ§МЋИДЙЄЃЌМгАрМгЕуЩњВњвНгУЗРЛЄЗўЃЌЮЊЗРПивЛЯпжњСІЃЎвдЯТЪЧИУЙЋЫОвдЭљЕФЪаГЁЕїВщЃЌЗЂЯжИУЙЋЫОЗРЛЄЗўЕФШеЯњЪлСПyЃЈЬзЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉжЎМфТњзувЛДЮКЏЪ§ЙиЯЕЃЌШчЯТЭМЫљЪОЃЌЙигкШеЯњЪлРћШѓwЃЈдЊЃЉКЭЯњЪлЕЅМлxЃЈдЊЃЉЕФМИзщЖдгІжЕШчЯТБэЃК
ЯњЪлЕЅМлxЃЈдЊЃЉ | 85 | 95 | 105 |
ШеЯњЪлРћШѓwЃЈдЊЃЉ | 875 | 1875 | 1875 |
ЃЈзЂЃКШеЯњЪлРћШѓЃНШеЯњЪлСПЁСЃЈЯњЪлЕЅМлвЛГЩБОЕЅМлЃЉЃЉ
ЃЈ1ЃЉЧѓyЙигкxЕФКЏЪ§НтЮіЪНЃЈВЛвЊЧѓаДГіxЕФШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ2ЃЉИљОнКЏЪ§ЭМЯѓКЭБэИёЫљЬсЙЉЕФаХЯЂЃЌЬюПеЃК
ИУЙЋЫОЩњВњЕФЗРЛЄЗўЕФГЩБОЕЅМлЪЧЁЁ ЁЁдЊЃЌЕБЯњЪлЕЅМлxЃНЁЁ ЁЁдЊЪБЃЌШеЯњЪлРћШѓwзюДѓЃЌзюДѓжЕЪЧЁЁ ЁЁдЊЃЛ
ЃЈ3ЃЉИУЙЋЫОИДЙЄвдКѓЃЌдкеўИЎВПУХЕФАяжњЯТЃЌдВФСЯВЩЙКГЩБОБШвдЭљгаСЫЯТНЕЃЌЦНОљЦ№РДЃЌУПЩњВњвЛЬзЗРЛЄЗўЃЌГЩБОБШвдЧАЯТНЕ5дЊЃЎИУЙЋЫОМЦЛЎПЊеЙПЦММДДаТЃЌвдНЕЕЭИУВњЦЗЕФГЩБОЃЌШчЙћдкНёКѓЕФЯњЪлжаЃЌШеЯњЪлСПгыЯњЪлЕЅМлШдДцдкЃЈ1ЃЉжаЕФЙиЯЕЃЎШєЯыЪЕЯжЯњЪлЕЅМлЮЊ90дЊЪБЃЌШеЯњЪлРћШѓВЛЕЭгк3750дЊЕФЯњЪлФПБъЃЌИУВњЦЗЕФГЩБОЕЅМлгІВЛГЌЙ§ЖрЩйдЊЃП