��Ŀ����
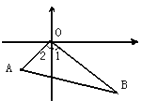
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�![]() ������ԭ�㣬������
������ԭ�㣬������![]() ��
��![]() �������ύ�ڵ�
�������ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ������
������![]() ����
����![]() �ֱ���
�ֱ���![]() ���е�.
���е�.![]() ����
����![]() ʼ�ձ��ֱ�
ʼ�ձ��ֱ�![]() ������
������![]() ����
����![]() ������
������![]() ����
����![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
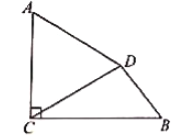
��1����գ�![]() �ij��� ��
�ij��� ��![]() �Ķ����� ��
�Ķ����� ��
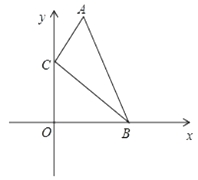
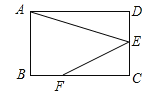
��2����ͼ2����![]() ������
������![]()
����֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
���жϵ�![]() �Ƿ��������ߵĶԳ����ϣ���˵�����ɣ�
�Ƿ��������ߵĶԳ����ϣ���˵�����ɣ�
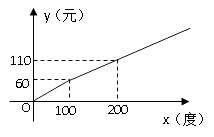
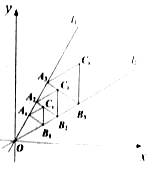
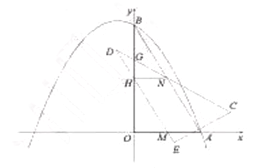
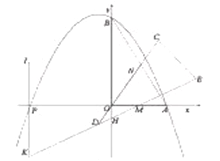
��3����ͼ3������![]() ������
������![]() ʱ����ʱ��
ʱ����ʱ��![]() ���
���![]() �غϣ�������
�غϣ�������![]() ��
��![]() ����
����![]() �ӳ������ڵ�
�ӳ������ڵ�![]() ���ӳ�
���ӳ�![]() ����
����![]() ��ʹ
��ʹ![]() ������
������![]() ��
��![]() ����
����![]() ��ȡһ��
��ȡһ��![]() ��ʹ��
��ʹ��![]() ����
����![]() ��ֱ��
��ֱ��![]() ��ͬ�ࣩ������
��ͬ�ࣩ������![]() ����ֱ��д����
����ֱ��д����![]() ��.
��.
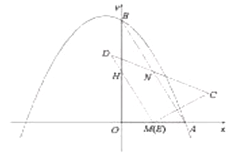
���𰸡�(1)8��30����2�����������������D�ڸ������ߵĶԳ����ϣ����������������3��12![]() .
.
��������
�����������1�����������ߵĽ���ʽ![]() ��õ�A������Ϊ��8��0������B������Ϊ��0��8
��õ�A������Ϊ��8��0������B������Ϊ��0��8![]() �������ɵ�OA=8,����������Ǻ����Ķ��弴�����
�������ɵ�OA=8,����������Ǻ����Ķ��弴�����![]() =30������2������
=30������2������![]() ������ƽ���߷��߶γɱ��������ɵ�
������ƽ���߷��߶γɱ��������ɵ�![]() ,����OM=AM,�ɵ�OH=BH,����BN=AN�����������ε���λ�߶����ɵ�
,����OM=AM,�ɵ�OH=BH,����BN=AN�����������ε���λ�߶����ɵ�![]() �������ж��ı���AMHN��ƽ���ı��Σ�����D�ڸ������ߵĶԳ����ϣ���ͼ������D��DR
�������ж��ı���AMHN��ƽ���ı��Σ�����D�ڸ������ߵĶԳ����ϣ���ͼ������D��DR![]() y���ڵ�R����
y���ڵ�R����![]() �ɵ���NHB=��AOB=90������
�ɵ���NHB=��AOB=90������![]() ���ɵ���DHB=��OBA=30��������
���ɵ���DHB=��OBA=30��������![]() ������ȫ�������ε����ʿɵ���HDG=��OBA=30�������ɵ���HDN=��HND������DH=HN=
������ȫ�������ε����ʿɵ���HDG=��OBA=30�������ɵ���HDN=��HND������DH=HN=![]() OA=4����Rt��DHR�У�DR=
OA=4����Rt��DHR��DR=![]() DH=
DH=![]() ,�����ж���D�ĺ�����Ϊ-2.���������ߵĶԳ���Ϊֱ��
,�����ж���D�ĺ�����Ϊ-2.���������ߵĶԳ���Ϊֱ��![]() ��������D�ڸ������ߵĶԳ����ϣ�
��������D�ڸ������ߵĶԳ����ϣ�
���������(1)8��30��
��2����֤������![]() ��
��
��![]() ,
,
����OM=AM,
��OH=BH,
����BN=AN
��![]()
���ı���AMHN��ƽ���ı���
����D�ڸ������ߵĶԳ����ϣ��������£�
��ͼ������D��DR![]() y���ڵ�R��
y���ڵ�R��
��![]()
���NHB=��AOB=90����
��![]() ��
��
���DHB=��OBA=30����
����![]()
���HDG=��OBA=30����
���HDG=��DHB=30����
���HGN=2��HDG=60����
���HNG=90��-��HGN=90��-60��=30����
���HDN=��HND��
��DH=HN=![]() OA=4
OA=4
��Rt��DHR��DR=![]() DH=
DH=![]() ,
,
����D�ĺ�����Ϊ-2.
���������ߵĶԳ���Ϊֱ��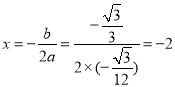 ��
��
����D�ڸ������ߵĶԳ�����.
(3)12![]() .
.
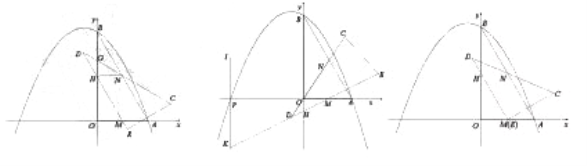

����Ŀ��Ϊ�˽�һ���˽�ijУ���꼶ѧ�����������������������ʦ�Ը�У���꼶��1����50λѧ������һ���������������ԣ��Բ�������Ϊ���������Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ��������ʾ��
��� | ����x | Ƶ��(����) |
��1�� | 80��x��100 | 6 |
��2�� | 100��x��120 | 8 |
��3�� | 120��x��140 | a |
��4�� | 140��x��160 | 18 |
��5�� | 160��x��180 | 6 |
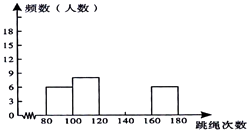
����ͼ������������⣺
��1�������a��ֵ��
��2�����Ƶ���ֲ�ֱ��ͼ����������
��3������һ������������������120�ε�Ϊ���Բ��ϸ����У���꼶��1000���У�һ��������
���ϸ��������Լ�ж��٣�