题目内容
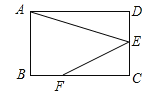
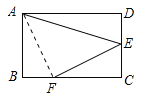
【题目】如图，在矩形ABCD中，点E是CD的中点，点F是BC上一点，且FC=2BF，连接AE，EF．若AB=2，AD=3，则cos∠AEF的值是 ．
【答案】
．
【解析】
试题分析：连接AF，如图所示：
∵四边形ABCD是矩形，∴∠B=∠C=90°，CD=AB=2，BC=AD=3，∵FC=2BF，∴BF=1，FC=2，∴AB=FC，∵E是CD的中点，∴CE=
CD=1，∴BF=CE，在△ABF和△FCE中，∵AB=FC，∠B=∠C，BF=CE，∴△ABF≌△FCE（SAS），∴∠BAF=∠CFE，AF=FE，∵∠BAF+∠AFB=90°，∴∠CFE+∠AFB=90°，∴∠AFE=180°﹣90°=90°，∴△AEF是等腰直角三角形，∴∠AEF=45°，∴ocs∠AEF=；故答案为：．
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹，成绩如表：
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且 
=8，S乙2=1.8，S甲2=1.2，根据上述信息完成下列问题：
（1）乙运动员射击训练成绩的众数是 ， 中位数是 ．
（2）求甲运动员射击成绩的平均数，并判断甲、乙两人在本次射击成绩的稳定性．
