Question

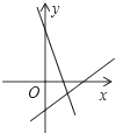
【题目】某地区的电力资源丰富，并且得到了较好的开发。该地区一家供电公司为了鼓励居民用电，采用分段计费的方法来计算电费. 月用电量x（度）与相应电费y（元）之间的函数图像如图所示.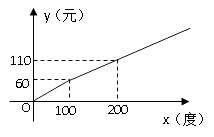
（1）月用电量为100度时，应交电费元；
（2）当x≥100时，求y与x之间的函数关系式；
（3）月用电量为260度时，应交电费多少元？

Answer 1

【答案】
（1）60
（2）解：当用电量大于100度时,超出的部分按（110-60）/(200-100)=0.5元/度

月用电量大于100度时,函数关系式为：

y=60+（x-100）×0.5

化简：y=60+0.5x-50

=0.5x+10 （x≥100）

（3）解：得出月用电量为260度时,令x=260,电费为

y=0.5×260+10=140元.

【解析】（1）根据函数图象，当x=100时，可直接从函数图象上读出y的值；（2）由图象知，当用电量大于100度时,超出的部分按（110-60）/(200-100)=0.5元/度，由此得出y=60+（x-100）×0.5，化简得到y与x之间的函数关系式；（3）把x=260代入第（2）问的函数关系式即可.