ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ«κ‘ΡΕΝœ¬Ν–≤ΡΝœΘΚ
Έ ΧβΘΚ»γΆΦ1Θ§‘ΎΒ»±Ώ»ΐΫ«–ΈABCΡΎ”–“ΜΒψPΘ§«“PA=2Θ§PB=![]() Θ§PC=1ΓΔ«σΓœBPCΕ» ΐΒΡ¥σ–ΓΚΆΒ»±Ώ»ΐΫ«–ΈABCΒΡ±Ώ≥ΛΘ°
Θ§PC=1ΓΔ«σΓœBPCΕ» ΐΒΡ¥σ–ΓΚΆΒ»±Ώ»ΐΫ«–ΈABCΒΡ±Ώ≥ΛΘ°
άνΟςΆ§―ßΒΡΥΦ¬Ζ «ΘΚΫΪΓςBPC»ΤΒψBΡφ ±’κ–ΐΉΣ60ΓψΘ§Μ≠≥ω–ΐΉΣΚσΒΡΆΦ–ΈΘ®»γΆΦ2Θ©Θ§Ν§Ϋ”PPΓδΘ§Ω…ΒΟΓςPΓδPC «Β»±Ώ»ΐΫ«–ΈΘ§ΕχΓςPPΓδA”÷ «÷±Ϋ«»ΐΫ«–ΈΘ®”…Ι¥Ι…Ε®άμΒΡΡφΕ®άμΩ…÷ΛΘ©Θ§¥”ΕχΒΟΒΫΓœBPC=ΓœAPΓδB=__________ΘΜΘ§ΫχΕχ«σ≥ωΒ»±ΏΓςABCΒΡ±Ώ≥ΛΈΣ__________ΘΜ
Έ ΧβΒΟΒΫΫβΨωΘ°
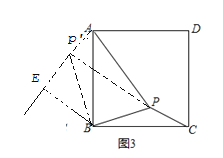
«κΡψ≤ΈΩΦάνΟςΆ§―ßΒΡΥΦ¬ΖΘ§ΧΫΨΩ≤ΔΫβΨωœ¬Ν–Έ ΧβΘΚ»γΆΦ3Θ§‘Ύ’ΐΖΫ–ΈABCDΡΎ”–“ΜΒψPΘ§«“PA=![]() Θ§BP=
Θ§BP=![]() Θ§PC=1Θ°«σΓœBPCΕ» ΐΒΡ¥σ–ΓΚΆ’ΐΖΫ–ΈABCDΒΡ±Ώ≥ΛΘ°
Θ§PC=1Θ°«σΓœBPCΕ» ΐΒΡ¥σ–ΓΚΆ’ΐΖΫ–ΈABCDΒΡ±Ώ≥ΛΘ°

ΓΨ¥πΑΗΓΩΘ®1Θ©150ΓψΘ§![]() ΘΜΘ®2Θ©135ΓψΘ§
ΘΜΘ®2Θ©135ΓψΘ§![]()
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©άϊ”Ο–ΐΉΣΒΡ–‘÷ Θ§ΒΟΒΫ»ΪΒ»»ΐΫ«–Έ.
(2)άϊ”ΟΘ®1Θ©÷–ΒΡΫβΧβΥΦ¬ΖΘ§Α―ΓςBPC,–ΐΉΣΘ§ΒΫΓςBPΓ·A,Ν§Ϋ”PPΓ·,BPΓ·Θ§»ί“Ή÷ΛΟςΓςAPPΓ· «÷±Ϋ«»ΐΫ«–ΈΘ§ΓœBPΓ·E=45ΓψΘ§“―÷Σ±ΏBPΓ·=BP=![]() Θ§BE=BPΓ·=1Θ§Ι¥Ι…Ε®άμΩ…«σΒΟ’ΐΖΫ–Έ±Ώ≥Λ.
Θ§BE=BPΓ·=1Θ§Ι¥Ι…Ε®άμΩ…«σΒΟ’ΐΖΫ–Έ±Ώ≥Λ.
Θ®1Θ©150Γψ![]()
Θ®2Θ©ΫΪΓςBPC»ΤΒψBΡφ ±’κ–ΐΉΣ90ΓψΘ§ΒΟΓςBPΓδAΘ§‘ρΓςBPCΓ’ΓςBPΓδAΘ°
ΓύAPΓδ=PC=1Θ§BP=BPΓδ=![]() ΘΜ
ΘΜ
Ν§Ϋ”PPΓδΘ§‘ΎRtΓςBPΓδP÷–Θ§
ΓΏBP=BPΓδ=![]() Θ§ΓœPBPΓδ=90ΓψΘ§
Θ§ΓœPBPΓδ=90ΓψΘ§
ΓύPPΓδ=2Θ§ΓœBPΓδP=45ΓψΘΜ
‘ΎΓςAPΓδP÷–Θ§APΓδ=1Θ§PPΓδ=2Θ§AP=![]() Θ§
Θ§
ΓΏ![]() Θ§Φ¥APΓδ2+PPΓδ2=AP2ΘΜ
Θ§Φ¥APΓδ2+PPΓδ2=AP2ΘΜ
ΓύΓςAPΓδP «÷±Ϋ«»ΐΫ«–ΈΘ§Φ¥ΓœAPΓδP=90ΓψΘ§
ΓύΓœAPΓδB=135ΓψΘ§
ΓύΓœBPC=ΓœAPΓδB=135ΓψΘ°
ΙΐΒψBΉςBEΓΆAPΓδΘ§ΫΜAPΓδΒΡ―”≥ΛœΏ”ΎΒψEΘΜ‘ρΓςBEPΓδ «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύΓœEPΓδB=45ΓψΘ§
ΓύEPΓδ=BE=1Θ§
ΓύAE=2ΘΜ
Γύ‘ΎRtΓςABE÷–Θ§”…Ι¥Ι…Ε®άμΘ§ΒΟAB=![]() ΘΜ
ΘΜ
ΓύΓœBPC=135ΓψΘ§’ΐΖΫ–Έ±Ώ≥ΛΈΣ![]() Θ°
Θ°