Question

【题目】已如边长为的正方形ABCD中，C（0，5），点A在x轴上，点B在反比例函数y=（x＞0，m＞0）的图象上，点D在反比例函数y=（x＜0，n＜0）的图象上，那么m+n=______．

Answer 1

【答案】±5

【解析】

由勾股定理可求点A坐标，分两种情况讨论，利用全等三角形的判定和性质求出B、D的坐标，即可求解．

解：设点A（x，0）

∴AC2=OA2+OC2，

∴26=25+OA2，

∴OA=1

∴点A（1，0），或（-1，0）

当点A（1，0）时，

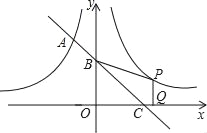
如图，过点B作BF⊥x轴，过点C作CE⊥y轴，与BF交于点E，过点D作DH⊥x轴，交CE于点G，

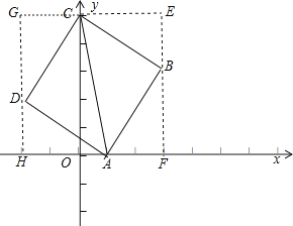
∵∠CBE+∠ABF=90°，且∠CBE+∠ECB=90°

∴∠ECB=∠ABF，且BC=AB，∠E=∠AFB=90°

∴△ABF≌△BCE（AAS）

∴BE=AF，BF=CE

∵OF=OA+AF

∴CE=OF=1+BE=BF

∴BF+BE=1+BE+BE=5

∴BE=2，

∴BF=3

∴点B坐标（3，3）

∴m=3×3=9，

∵A（1，0）, C（0，5）, B（3，3）,

∴点D(1+0-3，0+5-3)，即（-2，2）

∴n=-2×2=-4

∴m+n=5

若点A（-1，0）时，

同理可得：B（2，2）,D（-3，3）,

∴m=4，n=-9

∴m+n=-5

故答案为：±5