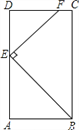
��Ŀ����
����Ŀ����֪����������y=![]() ��ͼ����A��x1��y1����B��x2��y2����x1��x2��
��ͼ����A��x1��y1����B��x2��y2����x1��x2��
��1����A��4��n����B��n+![]() ��3�������������ı���ʽ��
��3�������������ı���ʽ��
��2����m=1��
�ٵ�x2=1ʱ��ֱ��д��y1��ȡֵ��Χ��
�ڵ�x1��x2��0��p=![]() ��q=
��q=![]() �����ж�p��q�Ĵ�С��ϵ����˵�����ɣ�
�����ж�p��q�Ĵ�С��ϵ����˵�����ɣ�
��3������A��B�����ֱ��y=x+2��y�ύ�ڵ�C������BO���ǡ�COB�����ΪS����![]() ��S��1����m��ȡֵ��Χ��
��S��1����m��ȡֵ��Χ��
���𰸡���1��y=![]() ����2���ٵ�0��x1��1ʱ��y1��1����x1��0ʱ��y1��0����p��q������������3��
����2���ٵ�0��x1��1ʱ��y1��1����x1��0ʱ��y1��0����p��q������������3��![]() ��m��3��-1��m��-
��m��3��-1��m��-![]()
��������
��1������A��B��������뷴������������ʽ�У����������鼴�ɵó����ۣ�
��2���ȵó���������������ʽ��
���ȵó�x1=![]() ���ٷ�����������ۼ��ɵó����ۣ�
���ٷ�����������ۼ��ɵó����ۣ�
���ȱ�ʾ��y1=![]() ��y2=
��y2=![]() �������ó�p=
�������ó�p=![]() ���������������ɵó����ۣ�
���������������ɵó����ۣ�
��3������m��ʾ��x2=-1+![]() ���������C���꣬������x2��ʾ��S���ٷ����������
���������C���꣬������x2��ʾ��S���ٷ����������![]() ��S��1ȷ����x2�ķ�Χ�����ɵó�-1+
��S��1ȷ����x2�ķ�Χ�����ɵó�-1+![]() �ķ�Χ�����ɵó�m�ķ�Χ��
�ķ�Χ�����ɵó�m�ķ�Χ��
�⣺��1����A��4��n����B��n+![]() ��3���ڷ���������y=
��3���ڷ���������y=![]() ��ͼ���ϣ�
��ͼ���ϣ�
��4n=3��n+![]() ��=m��
��=m��
��n=1��m=4��
�������������ı���ʽΪy=![]() ��
��
��2����m=1��
�������������ı���ʽΪy=![]() ��
��
����ͼ1����B��x2��y2���ڷ���������y=![]() ��ͼ���ϣ�
��ͼ���ϣ�
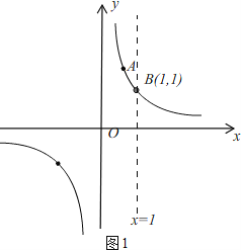
��y2=1��
��B��1��1����
��A��x1��y1���ڷ���������y=![]() ��ͼ���ϣ�
��ͼ���ϣ�
��y1=![]() ��
��
��x1=![]() ��
��
��x1��x2��x2=1��
��x1��1��
��0��x1��1ʱ��y1��1��
��x1��0ʱ��y1��0��
��p��q�����ɣ�������������y=![]() ��ͼ����A��x1��y1����B��x2��y2����
��ͼ����A��x1��y1����B��x2��y2����
��y1=![]() ��y2=
��y2=![]() ��
��
��p=![]() =
=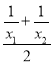 =
=![]() ��
��
��q=![]() ��
��
��p-q=![]() -
-![]() =
=![]() =
=![]() ��
��
��x1��x2��0��
����x1+x2��2��0��x1x2��0��x1+x2��0��
��![]() ��0��
��0��
��p-q��0��
��p��q��
��3������B��x2��y2����ֱ��AB��y=x+2�ϣ�Ҳ���ڷ���������y=![]() ��ͼ���ϣ�
��ͼ���ϣ�
��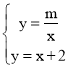 ����ã�x=-1
����ã�x=-1![]() ��
��
��x1��x2��
��x2=-1+![]()
��ֱ��AB��y=x+2��y���ཻ�ڵ�C��
��C��0��2����
��m��0ʱ����ͼ2��

��A��x1��y1����B��x2��y2����x1��x2����
����B��������0��
����x2��0
��S=![]() OCx2=
OCx2=![]() ��2��x2=x2��
��2��x2=x2��
��![]() ��S��1��
��S��1��
��![]() ��x2��1��
��x2��1��
��![]() ��-1+
��-1+![]() ��1��
��1��
��![]() ��m��3��
��m��3��
��m��0ʱ����ͼ3����A��x1��y1����B��x2��y2����x1��x2����
����B�ĺ�����С��0��

����x2��0
��S=![]() OC|x2|=-
OC|x2|=-![]() ��2��x2=-x2��
��2��x2=-x2��
��![]() ��S��1��
��S��1��
��![]() ��-x2��1��
��-x2��1��
��-1��x2��-![]() ��
��
��-1��-1+![]() ��-
��-![]() ��
��
��-1��m��-![]() ��
��
������![]() ��S��1ʱ��m��ȡֵ��ΧΪ
��S��1ʱ��m��ȡֵ��ΧΪ![]() ��m��3��-1��m��-
��m��3��-1��m��-![]() ��
��