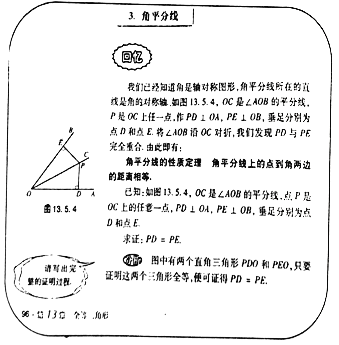
��Ŀ����
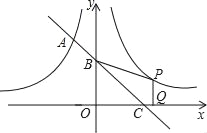
����Ŀ����ͼ��һ�κ�����ͼ���뷴��������![]() ��ͼ���ཻ��A�㣬��y�ᡢx��ֱ��ཻ��B��C���㣬��C��2��0������x����1ʱ��һ�κ���ֵ���ڷ���������ֵ����x����1ʱ��һ�κ���ֵС�ڷ���������ֵ��
��ͼ���ཻ��A�㣬��y�ᡢx��ֱ��ཻ��B��C���㣬��C��2��0������x����1ʱ��һ�κ���ֵ���ڷ���������ֵ����x����1ʱ��һ�κ���ֵС�ڷ���������ֵ��
(1)��һ�κ����Ľ���ʽ��
(2)�躯��y2=![]() ��ͼ����
��ͼ����![]() ��ͼ�����y��Գƣ���y2=
��ͼ�����y��Գƣ���y2=![]() ��ͼ����ȡһ��P��P��ĺ��������2������P��PQ�Ax�ᣬ������Q�����ı���BCQP���������2����P������꣮
��ͼ����ȡһ��P��P��ĺ��������2������P��PQ�Ax�ᣬ������Q�����ı���BCQP���������2����P������꣮
���𰸡���1��һ�κ�������ʽΪy= �Cx+2. ��2��P��![]() ��
��![]() ��
��
��������
����1����x��-1ʱ��һ�κ���ֵ���ڷ���������ֵ����x��-1ʱ��һ�κ���ֵС�ڷ���������ֵ��
��A��������-1��
��A��-1��3����
��һ�κ����Ľ���ʽΪy=kx+b����ֱ�߹�A��C��
��![]() ��
��
��֮��![]() ��
��
��һ�κ����Ľ���ʽΪy=-x+2��
��2����y2��![]() ��ͼ����y1����
��ͼ����y1����![]() (x<0)��ͼ�����y��Գƣ�
(x<0)��ͼ�����y��Գƣ�
��y2=![]() ��x��0����
��x��0����
��B����ֱ��y=-x+2��y��Ľ��㣬
��B��0��2����
��p��n��![]() ��n��2��
��n��2��
S�ı���BCQP=S�ı���OQPB-S��OBC=2��
��![]() ��2+
��2+![]() ��n-
��n-![]() ��2��2=2��
��2��2=2��
n=![]() ��
��
��P![]()

��ϰ��ϵ�д�
�����Ŀ