��Ŀ����
����Ŀ����������L��y=ax2+bx+c��a��b��c�dz�������abc��0����ֱ��l������y���ϵ�ͬһ�㣬��������L�Ķ�����ֱ��l�ϣ���ƴ�������L��ֱ��l���С�һ��һ·����ϵ�����ҽ�ֱ��l����������L�ġ�·�ߡ���������L����ֱ��l�ġ����ߡ���
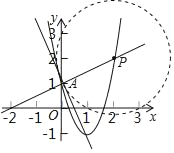
��1������·�ߡ�l�ı���ʽΪy=��x+2�����ġ����ߡ�L�Ķ����ڷ���������y=![]() ��ͼ���ϣ����ߡ�L�ı���ʽ��
��ͼ���ϣ����ߡ�L�ı���ʽ��
��2�����������y=mx2��2mx+m��1��ֱ��y=nx+1���С�һ��һ·����ϵ����m��n��ֵ��
��3���裨2���еġ����ߡ�L�����ġ�·�ߡ�l��y���ϵĽ���ΪA����֪��PΪ�����ߡ�L�ϵĵ㣬���Ե�PΪԲ�ĵ�Բ�롰·�ߡ�l�����ڵ�Aʱ�������P������
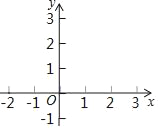
���𰸡���1�� �����ߡ�L�Ľ���ʽΪy=x2��2x+2����2��m��n��ֵ�ֱ�Ϊ2����2����3��P������Ϊ��![]() ��
��![]() ����
����
��������
��1�������¶��壬ͨ���ⷽ����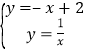 �ô��ߡ�L�Ķ�������Ϊ��1��1�����������·�ߡ�l��y��Ľ�������Ϊ��0��2�����������⡱���ߡ�L�����㣨0��2����Ȼ�����ô���ϵ��������ߡ�L�Ľ���ʽ��
�ô��ߡ�L�Ķ�������Ϊ��1��1�����������·�ߡ�l��y��Ľ�������Ϊ��0��2�����������⡱���ߡ�L�����㣨0��2����Ȼ�����ô���ϵ��������ߡ�L�Ľ���ʽ��
��2����ȷ��ֱ��y=nx+1��y��Ľ�������Ϊ��0��1���������¶���ѣ�0��1������y=mx2��2mx+m��1�ɵ�m=2�������ö��κ��������ʵõ������ߵĶ�������Ϊ��1����1����
Ȼ��Ѷ����������y=nx+1�пɵõ�n��ֵ��
��3���ɣ�2����A��0��1������PA��ֱ��y=��2x+1����������P����ͼ��������һ�κ�����ֱһ����ϵ���Ĺ�ϵ�õ�ֱ��PA�Ľ���ʽΪy=![]() x+1��Ȼ��ͨ���ⷽ����
x+1��Ȼ��ͨ���ⷽ����  ��P�����꣮
��P�����꣮
��1���ⷽ����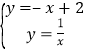 ��
��![]() ������ߡ�L�Ķ�������Ϊ��1��1����
������ߡ�L�Ķ�������Ϊ��1��1����
��x=0ʱ��y=��x+2=2����·�ߡ�l��y��Ľ�������Ϊ��0��2����
�������⡱���ߡ�L�����㣨0��2����
�衰���ߡ�L�Ľ���ʽΪy=a��x��1��2+1��
�ѣ�0��2�������a+1=2�����a=1��
�ࡰ���ߡ�L�Ľ���ʽΪy=��x��1��2+1����y=x2��2x+2��
��2����x=0ʱ��y=nx+1=1����ֱ��y=nx+1��y��Ľ�������Ϊ��0��1����
�ѣ�0��1������y=mx2��2mx+m��1��m��1=1�����m=2��
�������߽���ʽΪy=2x2��4x+1��
��y=��x��1��2��1��
�������ߵĶ�������Ϊ��1����1����
�ѣ�1����1������y=nx+1��n+1=��1�����n=��2��
��m��n��ֵ�ֱ�Ϊ2����2��
��3���ɣ�2����A��0��1����
��PA��ֱ��y=��2x+1����������P����ͼ��
��ֱ��PA�Ľ���ʽΪy=![]() x+t��
x+t��
��A��0��1�������t=1��
��ֱ��PA�Ľ���ʽΪy=![]() x+1��
x+1��
�ⷽ����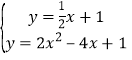 ��
��![]() ��
��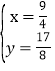 ��
��
��P��������![]() ��
��![]() ����
����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ������ij��ѧ�������й���У�����������ִ������ߡ����в����ݳ����ɼ�����ѡ��5��ѡ����ɳ��д����Ӻ��д����Ӳμ�ѧУ�����������Ӹ�ѡ����5��ѡ�ֵľ����ɼ���ͼ��ʾ��

��1������ͼʾ��д�±���
ƽ�������֣� | ��λ�����֣� | �������֣� | |
���в� | 85 | ||
���в� | 85 | 100 |
��2��������ӳɼ���ƽ��������λ���������ĸ��ӵľ����ɼ��Ϻã�
��3���������Ӿ����ɼ��ķ���ж���һ��������ѡ�ֳɼ���Ϊ�ȶ���