ћвƒњƒЏ»Ё
°Њћвƒњ°њ–°√чЇЌЉЄќїЌђ—І„ц ÷µƒ”∞„””ќѕЈ ±£ђЈҐѕ÷ґ‘”ЏЌђ“їќпће£ђ”∞„”µƒіу–°”лєв‘іµљќпћеµƒЊајл”–єЎ.“тіЋ£ђЋы√«»ѕќ™£Їњ…“‘љи÷ъќпћеµƒ”∞„”≥§ґ»Љ∆Ћгєв‘іµљќпћеµƒќї÷√.”Џ «£ђЋы√«„цЅЋ“‘ѕ¬≥Ґ ‘.
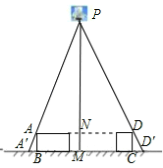
£®1£©»зЌЉҐў£ђіє÷±”ЏµЎ√жЈ≈÷√µƒ’эЈљ–ќњтЉ№ABCD£ђ±я≥§ABќ™30cm£ђ‘Џ∆д’э…ѕЈљ”–“їµ∆≈Ё£ђ‘Џµ∆≈Ёµƒ’’…дѕ¬£ђ’эЈљ–ќњтЉ№µƒЇбѕт”∞„”A°дB£ђD°дCµƒ≥§ґ»ЇЌќ™6cm.ƒ«√іµ∆≈ЁјлµЎ√жµƒЄяґ»ќ™ .
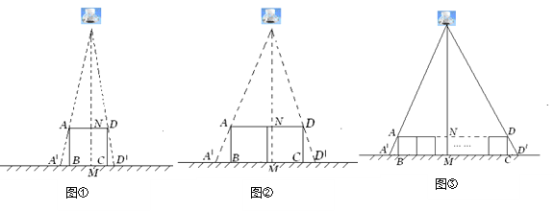 £®2£©≤їЄƒ±дҐў÷–µ∆≈ЁµƒЄяґ»£ђљЂЅљЄц±я≥§ќ™30cmµƒ’эЈљ–ќњтЉ№∞іЌЉҐЏ∞ЏЈ≈£ђ«лЉ∆ЋгіЋ ±Їбѕт”∞„”A°дB£ђD°дCµƒ≥§ґ»ЇЌќ™ґа…ў£њ
£®2£©≤їЄƒ±дҐў÷–µ∆≈ЁµƒЄяґ»£ђљЂЅљЄц±я≥§ќ™30cmµƒ’эЈљ–ќњтЉ№∞іЌЉҐЏ∞ЏЈ≈£ђ«лЉ∆ЋгіЋ ±Їбѕт”∞„”A°дB£ђD°дCµƒ≥§ґ»ЇЌќ™ґа…ў£њ
£®3£©”–nЄц±я≥§ќ™aµƒ’эЈљ–ќ∞іЌЉҐџ∞ЏЈ≈£ђ≤вµ√Їбѕт”∞„”A°дB£ђD°дCµƒ≥§ґ»ЇЌќ™b,«уµ∆≈ЁјлµЎ√жµƒЊајл.£®–і≥цљвћвєэ≥ћ£ђљбєы”√Їђa,b,nµƒіъ э љ±н Њ£©
°Њір∞Є°њ£®1£©180cm £®2£©12 cm (3) ![]()
°Њљвќц°њ ‘ћвЈ÷ќц£Ї£®1£©…иµ∆≈Ёµƒќї÷√ќ™µгP£ђ“„µ√°чPAD°„°чPA°дD°д£ђ…и≥цЋщ«уµƒќі÷™ э£ђјы”√ѕаЋ∆»эљ«–ќµƒґ‘”¶±яµƒ±»µ»”Џґ‘”¶Єяµƒ±»£ђњ…µ√µ∆≈ЁјлµЎ√жµƒЄяґ»£ї
£®2£©ЌђЈ®њ…µ√µљЇбѕт”∞„”A°дB£ђD°дCµƒ≥§ґ»ЇЌ£ї
£®3£©∞і’’ѕа”¶µƒ»эљ«–ќѕаЋ∆£ђјы”√ѕаЋ∆»эљ«–ќµƒґ‘”¶±яµƒ±»µ»”Џґ‘”¶Єяµƒ±»£ђ”√„÷ƒЄ±н Њ≥ц∆дЋыѕяґќ£ђЉіњ…µ√µљµ∆≈ЁјлµЎ√жµƒЊајл£Ѓ
љв£Ї£®1£©…иµ∆≈ЁјлµЎ√жµƒЄяґ»ќ™xcm£ђ
°яAD°ќA°дD°д£ђ
°а°ѕPAD=°ѕPA°дD°д£ђ°ѕPDA=°ѕPD°дA°д£Ѓ
°а°чPAD°„°чPA°дD°д£Ѓ
ЄщЊЁѕаЋ∆»эљ«–ќґ‘”¶Єяµƒ±»µ»”ЏѕаЋ∆±»µƒ–‘÷ £ђњ…µ√![]() £ђ
£ђ
°а![]() =
=![]() £ђ
£ђ
љвµ√x=180£Ѓ£®4Ј÷£©
£®2£©…иЇбѕт”∞„”A°дB£ђD°дCµƒ≥§ґ»ЇЌќ™ycm£ђ
Ќђјнњ…µ√°а![]() =
=![]() £ђ
£ђ
љвµ√y=12cm£ї£®3Ј÷£©
£®3£©Љ«µ∆≈Ёќ™µгP£ђ»зЌЉ£Ї
°яAD°ќA°дD°д£ђ°а°ѕPAD=°ѕPA°дD°д£ђ°ѕPDA=°ѕPD°дA°д£Ѓ
°а°чPAD°„°чPA°дD°д£Ѓ
ЄщЊЁѕаЋ∆»эљ«–ќґ‘”¶Єяµƒ±»µ»”ЏѕаЋ∆±»µƒ–‘÷ £ђњ…µ√![]() £®1Ј÷£©
£®1Ј÷£©
£®÷±љ”µ√≥ц»эљ«–ќѕаЋ∆їт±»јэѕяґќЊщ≤їњџЈ÷£©
…иµ∆≈ЁјлµЎ√жЊајлќ™x£ђ”…ћв“в£ђµ√PM=x£ђPN=x©Бa£ђAD=na£ђA°дD°д=na+b£ђ
°а![]() =1©Б
=1©Б![]()
![]() =1©Б
=1©Б![]()
x=![]() £®1Ј÷£©£Ѓ
£®1Ј÷£©£Ѓ