Question

【题目】已知AC是菱形ABCD的对角线，∠BAC＝60°，点E是直线BC上的一个动点，连接AE，以AE为边作菱形AEFG，并且使∠EAG＝60°，连接CG，当点E在线段BC上时，如图1，易证：AB＝CG＋CE.

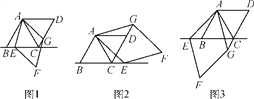
(1)当点E在线段BC的延长线上时(如图2)，猜想AB，CG，CE之间的关系并证明；

(2)当点E在线段CB的延长线上时(如图3)，直接写出AB，CG，CE之间的关系．

Answer 1

【答案】(1)AB＝CG－CE(2)AB＝CE－CG

【解析】试题分析：（1）根据菱形的性质可得AC=AD，AE=AG，然后证明∠DAG=∠CAE，可利用SAS证明△ACE≌△ADG，根据全等三角形的性质可得CE=DG，再根据线段的和差关系和等量代换可得答案；

（2）方法与（1）类似可证明△ACG≌△ABE，进而得到BE=CG，然后可得AB=CE﹣CG．

试题解析：(1)AB=CG-CE

∵AC是菱形ABCD的对角线且∠BAC=60°，∴AC=AD.

∵四边形AEFG菱形，∴AE=AG..

∵∠DAC=∠GAE ="60°," ∴∠DAG=∠CAE.

∴△ACE≌△ADG(SAS), ∴CE=DG..

∴AB=CD=CG-DG=CG-CE

(2). AB =" CE-" CG.

同理可证△ACG ≌△ABE(SAS),∴BE=CG..

∴AB ="CB=" CE- BE=CE-CG．