题目内容
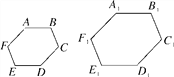
【题目】图中的两个多边形ABCDEF和A1B1C1D1E1F1相似(各字母已按对应关系排列),∠A=∠D1=135°,∠B=∠E1=120°,∠C1=95°.
(1)求∠F的度数;
(2)如果多边形ABCDEF和A1B1C1D1E1F1的相似比是1:1.5,且CD=15cm,求C1D1的长度.
【答案】 (1)∠F=115°;(2)C1D1=22.5cm.
【解析】试题分析:(1)、根据相似多边形的性质求出∠A、∠B、∠C、∠D、∠E的角度,然后根据五边形的内角和定理求出∠F的度数;(2)、相似多边形对应边的比值等于相似比,根据相似比求出线段的长度.
试题解析:(1)∵多边形ABCDEF和A1B1C1D1E1F1相似,∠A=∠D1=135°,∠B=∠E1=120°,∠C1=95°,
∴∠C=∠C1=95°,∠D=∠D1=135°,∠E=∠E1=120°.
由多边形内角和定理,得多边形ABCDEF的内角和为180°×(6-2)=720°,
∴∠F=720°-(135°+120°+95°+135°+120°)=115°;
(2)∵多边形ABCDEF和A1B1C1D1E1F1的相似比是1:1.5,且CD=15cm,
∴C1D1=15×1.5=22.5(cm).

练习册系列答案
相关题目