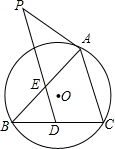
题目内容
如图,点C是以AB为直径的⊙O上的一点,AD与过点C的切线互相垂直,垂足为点D.
(1)求证:AC平分∠BAD;
(2)若CD=1,AC=
,求⊙O的半径长.

(1)求证:AC平分∠BAD;
(2)若CD=1,AC=
| 10 |

(1)证明:连接OC.
∵OA=OC,
∴∠ACO=∠CAO.
∵CD切⊙O于C,
∴OC⊥CD,
又∵AD⊥CD,
∴AD∥CO,
∴∠DAC=∠ACO,
∴∠DAC=∠CAO,
即AC平分∠BAD;
 (2)解法一:如图2①,过点O作OE⊥AC于E.
(2)解法一:如图2①,过点O作OE⊥AC于E.
在Rt△ADC中,AD=
=
=3,
∵OE⊥AC,
∴AE=
AC=
.
∵∠CAO=∠DAC,∠AEO=∠ADC=90°,
∴△AEO∽△ADC,
∴
=
,即
=
,
∴AO=
,即⊙O的半径为
.
 解法二:如图2②,连接BC.
解法二:如图2②,连接BC.
在Rt△ADC中,AD=
=
=3.
∵AB是⊙O直径,∴∠ACB=90°,
∵∠CAB=∠DAC,∠ACB=∠ADC=90°,
∴△ABC∽△ACD,
∴
=
,
即
=
,
∴AB=
,
∴AO=
AB=
×
=
,
即⊙O的半径为
.

∵OA=OC,
∴∠ACO=∠CAO.
∵CD切⊙O于C,
∴OC⊥CD,
又∵AD⊥CD,
∴AD∥CO,
∴∠DAC=∠ACO,
∴∠DAC=∠CAO,
即AC平分∠BAD;
 (2)解法一:如图2①,过点O作OE⊥AC于E.
(2)解法一:如图2①,过点O作OE⊥AC于E.在Rt△ADC中,AD=
| AC2-DC2 |
(
|
∵OE⊥AC,
∴AE=
| 1 |
| 2 |
| ||
| 2 |
∵∠CAO=∠DAC,∠AEO=∠ADC=90°,
∴△AEO∽△ADC,
∴
| AE |
| AD |
| AO |
| AC |
| ||||
| 3 |
| AO | ||
|
∴AO=
| 5 |
| 3 |
| 5 |
| 3 |
 解法二:如图2②,连接BC.
解法二:如图2②,连接BC.在Rt△ADC中,AD=
| AC2-DC2 |
(
|
∵AB是⊙O直径,∴∠ACB=90°,
∵∠CAB=∠DAC,∠ACB=∠ADC=90°,
∴△ABC∽△ACD,
∴
| AC |
| AD |
| AB |
| AC |
即
| ||
| 3 |
| AB | ||
|
∴AB=
| 10 |
| 3 |
∴AO=
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 3 |
| 5 |
| 3 |
即⊙O的半径为
| 5 |
| 3 |


练习册系列答案
相关题目