题目内容
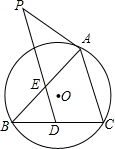
如图PA是△ABC的外接圆O的切线，A是切点，PD∥AC，且PD与AB、AC分别相交于E、D．
求证：（1）∠PAE=∠BDE；
（2）EA•EB=ED•EP．
求证：（1）∠PAE=∠BDE；
（2）EA•EB=ED•EP．
证明：如右图所示，
（1）∵AP是切线，
∴∠PAE=∠ACB，
又∵PD∥AC，
∴∠PDB=∠BDE，
∴∠PAE=∠BDE；
（2）由（1）得∠PAE=∠BDE，
又∵∠AEP=∠DEB，
∴△AEP∽△DEB，
∴AE：PE=DE：BE，
∴EA•EB=ED•EP．
（1）∵AP是切线，
∴∠PAE=∠ACB，
又∵PD∥AC，
∴∠PDB=∠BDE，
∴∠PAE=∠BDE；
（2）由（1）得∠PAE=∠BDE，
又∵∠AEP=∠DEB，
∴△AEP∽△DEB，
∴AE：PE=DE：BE，
∴EA•EB=ED•EP．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
