题目内容
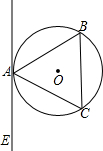
如图，AB是⊙O的直径，AB=10，DC切⊙O于点C，AD⊥DC，垂足为D，AD交⊙O于点E．
（1）求证：AC平分∠BAD；
（2）若sin∠BEC=
，求DC的长．
（1）求证：AC平分∠BAD；
（2）若sin∠BEC=
| 3 |
| 5 |
（1）证明：连接OC，由DC是切线得OC⊥DC；
又AD⊥DC，
∴AD∥OC，
∴∠DAC=∠ACO．
又由OA=OC得∠BAC=∠ACO，
∴∠DAC=∠BAC．
即AC平分∠BAD．
（2）方法一：∵AB为直径，
∴∠ACB=90°
又∵∠BAC=∠BEC，
∴BC=AB•sin∠BAC=AB•sin∠BEC=6．
∴AC=
=8．
又∵∠DAC=∠BAC=∠BEC，且AD⊥DC，
∴CD=AC•sin∠DAC=AC•sin∠BEC=
．
方法二：∵AB为直径，
∴∠ACB=90°．
又∵∠BAC=∠BEC，
∴BC=AB•sin∠BAC=AB•sin∠BEC=6．
∴AC=
=8．
又∵∠DAC=∠BAC，∠D=∠ACB=90°，
∴△ADC∽△ACB，
=
，即
=
，
解得DC=
．
又AD⊥DC，
∴AD∥OC，
∴∠DAC=∠ACO．
又由OA=OC得∠BAC=∠ACO，
∴∠DAC=∠BAC．
即AC平分∠BAD．
（2）方法一：∵AB为直径，
∴∠ACB=90°
又∵∠BAC=∠BEC，
∴BC=AB•sin∠BAC=AB•sin∠BEC=6．
∴AC=
| AB2-BC2 |
又∵∠DAC=∠BAC=∠BEC，且AD⊥DC，
∴CD=AC•sin∠DAC=AC•sin∠BEC=
| 24 |
| 5 |
方法二：∵AB为直径，
∴∠ACB=90°．
又∵∠BAC=∠BEC，
∴BC=AB•sin∠BAC=AB•sin∠BEC=6．
∴AC=
| AB2-BC2 |
又∵∠DAC=∠BAC，∠D=∠ACB=90°，
∴△ADC∽△ACB，
| DC |
| CB |
| AC |
| AB |
| DC |
| 6 |
| 8 |
| 10 |
解得DC=
| 24 |
| 5 |
练习册系列答案
相关题目
MAN的角平分线于E，过点E作ED⊥AM，垂足为D，反向延长ED交AN于F．
