题目内容
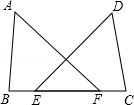
如图，点E，F在BC上，BE=CF，∠A=∠D，∠B=∠C，求证：AB=DC．
见解析
证明：∵点E，F在BC上，BE=CF，
∴BE+EF=CFR+EF，即BF=CE；
在△ABF和△DCE中，
，
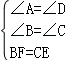∴△ABF≌△DCE（AAS），
∴AB=CD（全等三角形的对应边相等）．
∴BE+EF=CFR+EF，即BF=CE；
在△ABF和△DCE中，
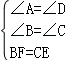，∴△ABF≌△DCE（AAS），
∴AB=CD（全等三角形的对应边相等）．
练习册系列答案
相关题目
题目内容
，
. 
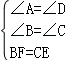，求OD的长．
