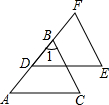
题目内容
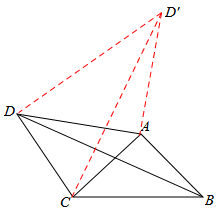
如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为 .
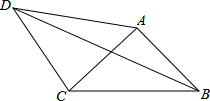

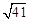 .
.试题分析:根据等式的性质,可得∠BAD与∠CAD′的关系,根据SAS,可得△BAD与△CAD′的关系,根据全等三角形的性质,可得BD与CD′的关系,根据勾股定理,可得答案:
如答图,作AD′⊥AD,AD′=AD,连接CD′,DD′,
∵∠ABC=∠ACB=45°,∴BA=BC.
∵∠BAC+∠CAD=∠DAD′+∠CAD,即∠BAD=∠CAD′,
在△BAD与△CAD′中,∵
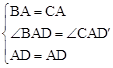 ,∴△BAD≌△CAD′(SAS).∴BD=CD′.
,∴△BAD≌△CAD′(SAS).∴BD=CD′.在Rt△ADD′中,由勾股定理得
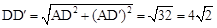 .
.∵∠D′DA=∠ADC=45°,∴∠D′DC=90°.
在Rt△CDD′中,由勾股定理得
 ,
,∴BD=CD′=
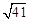 .
.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 (
( 为大于2的整数),连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连接BF和EG.
为大于2的整数),连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连接BF和EG. (
( 为常数),
为常数), 时,求FG的长;
时,求FG的长; ,矩形ABCD的面积为
,矩形ABCD的面积为 ,当
,当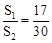 时,求
时,求
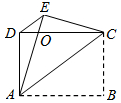
 ),则四边形ABCD的面积的最大值与最小值的差为___ ___.
),则四边形ABCD的面积的最大值与最小值的差为___ ___.