题目内容
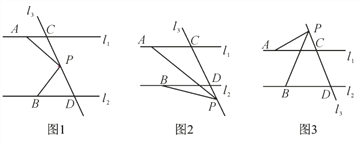
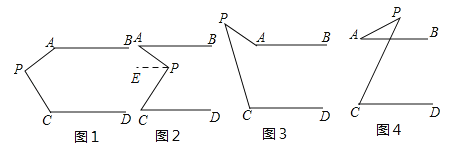
【题目】如图,已知AB∥CD,分别探讨下面四个图形中∠APC与∠PAB,∠PCD之间的关系,请你从所得到的关系中任选一个加以证明。
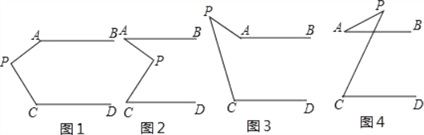
(1)在图1中,∠APC与∠PAB,∠PCD之间的关系是: .
(2)在图2中,∠APC与∠PAB,∠PCD之间的关系是: .
(3)在图3中,∠APC与∠PAB,∠PCD之间的关系是: .
(4)在图4中,∠APC与∠PAB,∠PCD之间的关系是: .
(5)在图 中,求证: .
【答案】答案见解析
【解析】试题分析:(1)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,即可求得答案;
(2)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;
(3)由AB∥CD,根据两直线平行,同位角线相等,以及三角形外角的性质,即可求得答案;
(4)由AB∥CD,根据两直线平行,同位角线相等,以及三角形外角的性质,即可求得答案.
试题解析:解:(1)∠APC+∠PAB+∠PCD=360°;
(2)∠APC=∠PAB+∠PCD;
(3)∠PAB=∠APC+∠PCD;
(4)∠PCD=∠APC+∠PAB.
(5)在图2中,求证:∠APC=∠PAB+∠PCD.
证明:过P点作PE∥AB,∴∠1=∠PAB.
又∵AB∥CD,PE∥CD,∴∠2=∠PCD,∴∠1+∠2=∠PAB+∠PCD,而∠APC=∠1+∠2,∴∠APC=∠PAB+∠PCD.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案【题目】八(1)班组织了一次汉字听写比赛,甲、乙两队各10人,其比赛成绩如下表(10分制):
甲队 | 7 | 8 | 9 | 10 | 10 | 10 | 10 | 9 | 9 | 8 |
乙队 | 7 | 7 | 8 | 9 | 10 | 10 | 9 | 10 | 10 | 10 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分.
(2)计算甲队的平均成绩和方差_
(3)已知乙队成绩的方差是1.4,则成绩较为整齐的是 队.