题目内容
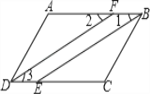
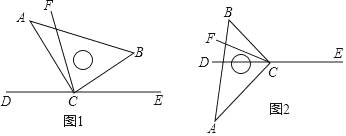
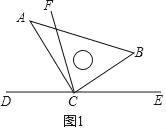
【题目】直角三角板ABC的直角顶点C在直线DE上,CF平分∠BCD.
(1)在图1中,若∠BCE=40°,求∠ACF的度数;
(2)在图1中,若∠BCE=α,直接写出∠ACF的度数(用含α的式子表示);
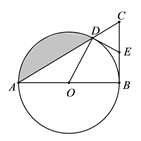
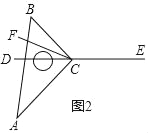
(3)将图1中的三角板ABC绕顶点C旋转至图2的位置,探究:写出∠ACF与∠BCE的度数之间的关系,并说明理由.
【答案】(1)∠ACF=20°;(2)∠ACF=![]() α;(3)∠ACF=
α;(3)∠ACF=![]() ∠BCE.理由见解析.
∠BCE.理由见解析.
【解析】试题分析:(1)由∠ACB=90°,∠BCE=40°,可得∠ACD,∠BCD的度数,再根据CF平分∠BCD,可得∠DCF的度数,继而可求得∠ACF=∠DCF﹣∠ACD=20°;
(2)由∠ACB=90°,∠BCE=α°,可得∠ACD=90°﹣α,∠BCD=180°﹣α,再根据CF平分∠BCD,从而可得∠DCF=90°﹣![]() α,继而可得∠ACF=
α,继而可得∠ACF=![]() α;
α;
(3)由点C在DE上,可得∠BCD=180°﹣∠BCE,再根据CF平分∠BCD,可得∠BCF=90°-![]() ∠BCE,再根据∠ACB=90°,从而有∠ACF=
∠BCE,再根据∠ACB=90°,从而有∠ACF=![]() ∠BCE.
∠BCE.
试题解析:(1)如图1,∵∠ACB=90°,∠BCE=40°,
∴∠ACD=180°﹣90°﹣40°=50°,∠BCD=180°﹣40°=140°,
又CF平分∠BCD,
∴∠DCF=∠BCF=![]() ∠BCD=70°,
∠BCD=70°,
∴∠ACF=∠DCF﹣∠ACD=70°﹣50°=20°;
(2)如图1,∵∠ACB=90°,∠BCE=α°,
∴∠ACD=180°﹣90°﹣α°=90°﹣α,∠BCD=180°﹣α,
又CF平分∠BCD,
∴∠DCF=∠BCF=![]() ∠BCD=90°﹣
∠BCD=90°﹣![]() α,
α,
∴∠ACF=90°﹣![]() α﹣90°+α=
α﹣90°+α=![]() α;
α;
(3)∠ACF=![]() ∠BCE.理由如下:
∠BCE.理由如下:
如图2,∵点C在DE上,
∴∠BCD=180°﹣∠BCE.
∵CF平分∠BCD,
∴∠BCF=![]() ∠BCD=
∠BCD=![]() (180°﹣∠BCE)=90°-
(180°﹣∠BCE)=90°-![]() ∠BCE.
∠BCE.
∵∠ACB=90°,
∴∠ACF=∠ACB﹣∠BCF=90°﹣(90°-![]() ∠BCE)=
∠BCE)=![]() ∠BCE.
∠BCE.
即:∠ACF=![]() ∠BCE.
∠BCE.

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案