Question

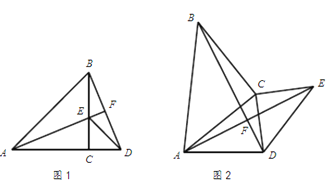
【题目】在△ABC和△DEC中，AC=BC，DC=EC，∠ACB=∠ECD=90°．

（1）如图1，当点A、C、D在同一条直线上时，AC=12，EC=5，

①求证：AF⊥BD； ②求AF的长度；

（2）如图2，当点A、C、D不在同一条直线上时，求证：AF⊥BD.

Answer 1

【答案】（1）①证明见解析；②；（2）证明见解析.

【解析】试题分析：（1）①证明△ACE≌△BCD，得到∠1=∠2，由对顶角相等得到∠3=∠4，所以∠BFE=∠ACE=90°，即可得结论；②根据勾股定理求出BD，利用△ABD的面积的两种表示方法，即可解答；（2）证明△ACE≌△BCD，得到∠1=∠2，又由∠3=∠4，得到∠BFA=∠BCA=90°，即可得结论.

试题解析：

（1）①证明：如图1，

∵在△ACE和△BCD中，

∴△ACE≌△BCD，

∴∠1=∠2，

∵∠3=∠4，

∴∠BFE=∠ACE=90°，

∴AF⊥BD．

②∵∠ECD=90°，BC=AC=12，DC=EC=5，

∴根据勾股定理得：BD=13，

∵S△ABD=ADBC=BDAF，

即

∴AF=．

（2）证明：如图2，

∵∠ACB=∠ECD，

∴∠ACB+∠ACD=∠ECD+∠ACD，

∴∠BCD=∠ACE，

在△ACE≌△BCD中

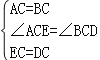
∴△ACE≌△BCD（SAS），

∴∠1=∠2，

∵∠3=∠4，

∴∠BFA=∠BCA=90°，

∴AF⊥BD．