题目内容
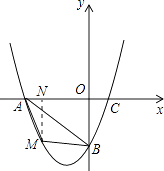
【题目】在平面直角坐标系中，已知抛物线经过A（﹣4，0），B（0，﹣4），C（2，0）三点．
（1）求抛物线的解析式；
（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值．
【答案】
（1）
解：设抛物线解析式为y=a（x+4）（x﹣2），
将B（0，﹣4）代入得：﹣4=﹣8a，即a= 
，
则抛物线解析式为y= （x+4）（x﹣2）= x2+x﹣4；
（2）
解：过M作MN⊥x轴，
将x=m代入抛物线得：y= m2+m﹣4，即M（m， m2+m﹣4），
∴MN=| m2+m﹣4|=﹣ m2﹣m+4，ON=﹣m，
∵A（﹣4，0），B（0，﹣4），∴OA=OB=4，
∴△AMB的面积为S=S△AMN+S梯形MNOB﹣S△AOB
= ×（4+m）×（﹣ m2﹣m+4）+ ×（﹣m）×（﹣ m2﹣m+4+4）﹣ ×4×4
=2（﹣ m2﹣m+4）﹣2m﹣8
=﹣m2﹣4m
=﹣（m+2）2+4，
当m=﹣2时，S取得最大值，最大值为4．
【解析】（1）根据抛物线与x轴的交点A与C坐标设出抛物线的二根式方程，将B坐标代入即可确定出解析式；（2）过M作x轴垂线MN，三角形AMB面积=梯形MNOB面积+三角形AMN面积﹣三角形AOB面积，求出即可．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
【题目】我们知道：等腰三角形、平行四边形、菱形、双曲线、抛物线．这些都是我们在初中学习阶段学过的几何图形或函数的图象，那么从它们之中随机抽取两个，得到的都是中心对称图形的概率是（ ）
A.
B.
C.
D.1
