Question

【题目】如图，在周长为12的菱形ABCD中，AE=1，AF=2，若P为对角线BD上一动点，则EP+FP的最小值为（ ）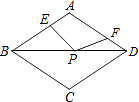

A.1
B.2
C.3
D.4

Answer 1

【答案】C
【解析】解：作F点关于BD的对称点F′，则PF=PF′，连接EF′交BD于点P．

∴EP+FP=EP+F′P．
由两点之间线段最短可知：当E、P、F′在一条直线上时，EP+FP的值最小，此时EP+FP=EP+F′P=EF′．
∵四边形ABCD为菱形，周长为12，
∴AB=BC=CD=DA=3，AB∥CD，
∵AF=2，AE=1，
∴DF=AE=1，
∴四边形AEF′D是平行四边形，
∴EF′=AD=3．
∴EP+FP的最小值为3．
故选：C．
【考点精析】通过灵活运用线段的基本性质和平行四边形的性质，掌握线段公理：所有连接两点的线中，线段最短．也可简单说成：两点之间线段最短；连接两点的线段的长度，叫做这两点的距离；线段的大小关系和它们的长度的大小关系是一致的；平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分即可以解答此题．