题目内容
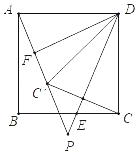
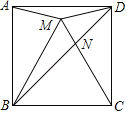
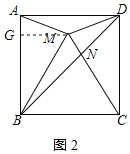
【题目】如图,点M是正方形ABCD内一点,△MBC是等边三角形,连接AM、MD.对角线BD交CM于点N,现有以下结论:①∠AMD=150°;②MA2=MNMC;③![]() ;④
;④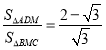 ,其中正确的结论有____(填写序号).
,其中正确的结论有____(填写序号).
【答案】①②③④.
【解析】
①先根据等边三角形得∠CMB=60°,再根据等腰三角形的性质得∠AMB=∠CMD=75°,最后根据周角的定义可得结论;
②证明△MND∽△MDC,列比例式可得结论;
③如图1,作辅助线,设NH=x,根据平行线分线段成比例定理得结论.
④如图2,设MG=x,根据直角三角形30度角的性质和勾股定理分别计算BC、AG、BG的长,根据面积公式计算可得结论;
∵△MBC是等边三角形,
∴∠MBC=∠MCB=∠CMB=60°,BM=BC,
∵四边形ABCD是正方形,
∴∠ABC=∠BCD=∠BAD=∠ADC=90°,AB=BC,
∴∠ABM=∠DCM=30°,
∵AB=BM,
∴∠AMB=∠BAM=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
同理∠CMD=∠CDM=75°,
∴∠AMD=360°﹣75°﹣75°﹣60°=150°;
故①正确;
∵四边形ABCD是正方形,
∴∠BDC=45°,
∴∠MDN=∠CDM﹣∠BDC=75°﹣45°=30°,
∵∠CMD=∠CMD,∠MDN=∠DCM=30°,
∴△MND∽△MDC,
∴![]() =
=![]() ,
,
∴DM2=MNMC,
∵∠BAD=∠ADC,∠BAM=∠CDM,
∴∠MAD=∠MDA,
∴MA=DM,
∴MA2=MNMC,
故②正确;
过N作NH⊥CD于H,设NH=x,如图1所示:
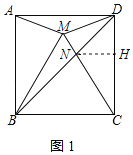
则NH⊥BC,∠NDH=∠DNH=45°,
∴NH=DH=x,
∵∠NCH=30°,∠CHN=90°
∴CN=2x,CH=![]() x,
x,
∵NH∥BC,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
故③正确;
过M作MG⊥AB于G,如图2所示:
设MG=x,
Rt△BGM中,∠GBM=30°,
∴BM=BC=AB=2x,BG=![]() x,
x,
∴AG=2x﹣![]() x,
x,
∴![]() =
=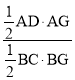 =
=![]() =
=![]() =
=![]() ,
,
故④正确;
故答案为:①②③④.

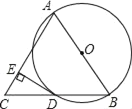
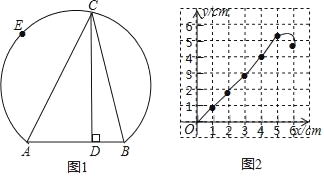
【题目】如图1所示,点E在弦AB所对的优弧上,且![]() 为半圆,C是
为半圆,C是![]() 上的动点,连接CA、CB,已知AB=4cm,设B、C间的距离为xcm,点C到弦AB所在直线的距离为y1cm,A、C两点间的距离为y2cm.
上的动点,连接CA、CB,已知AB=4cm,设B、C间的距离为xcm,点C到弦AB所在直线的距离为y1cm,A、C两点间的距离为y2cm.
小明根据学习函数的经验,分别对函数y1、y2岁自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整.
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1、y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 0.78 | 1.76 | 2.85 | 3.98 | 4.95 | 4.47 |
y2/cm | 4 | 4.69 | 5.26 | 5.96 | 5.94 | 4.47 |
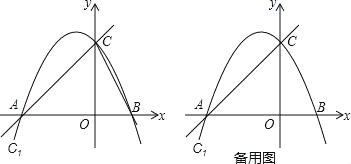
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1、y2的图象;
(3)结合函数图象,解决问题:
①连接BE,则BE的长约为 cm.
②当以A、B、C为顶点组成的三角形是直角三角形时,BC的长度约为 cm.