题目内容
【题目】如图，在平面直角坐标系xOy中，抛物线y＝x2+ax+b经过点A(﹣2，0)，B(1，3)．
(1)求抛物线的解析式；
(2)由图象直接写出：x取何值时，y随x的增大而减少；
(3)根据图象回答：x取何值时，y＞0．
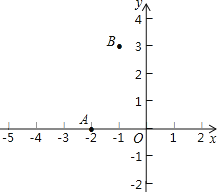
【答案】(1)y＝x2+6x+8；(2)x≤﹣3时，y随x的增大而减少；(3)x＜﹣4或x＞﹣2时，y＞0．
【解析】
（1）将点A、B的坐标代入抛物线的解析式，即可得到关于b、c的二元一次方程组，解方程组即可求解；
（2）先画出函数图象，由图象直接得到x的取值范围;
（3）观察图象,写出函数图象在x轴上方对应的x的取值范围即可．
(1)将点A、B的坐标代入抛物线的表达式得：
，解得：
，
故抛物线的表达式为：y＝x2+6x+8；
(2)由图象得：x≤﹣3时，y随x的增大而减少；
(3)由图象得：x＜﹣4或x＞﹣2时，y＞0．
练习册系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
