题目内容
【题目】已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AB=AC,连接AC,过点D作DE⊥AC,垂足为 E.
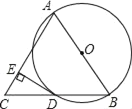
(1)求证:DC=BD;
(2)求证:DE为⊙O的切线;
(3)若AB=12,AD=6![]() ,连接OD,求扇形BOD的面积.
,连接OD,求扇形BOD的面积.
【答案】(1)见解析;(2)见解析;(3)6π
【解析】
(1)连接AD,根据圆周角定理得到∠ADB=90°,然后由三线合一可得结论;
(2)连接OD,证明OD∥AC,得到∠ODE=90°即可;
(3)根据三角函数的定义得到sinB=![]() =
=![]() =
=![]() ,求得∠B=60°,得到∠BOD=60°,根据扇形的面积公式即可得到结论.
,求得∠B=60°,得到∠BOD=60°,根据扇形的面积公式即可得到结论.
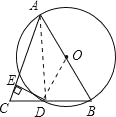
证明:(1)连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
又∵AB=AC,
∴DC=BD;
(2)连接OD,
∵OA=OB,CD=BD,
∴OD∥AC,
∴∠ODE=∠CED,
又∵DE⊥AC,
∴∠CED=90°,
∴∠ODE=90°,即OD⊥DE.
∴DE是⊙O的切线;
(3)∵AB=12,AD=6![]() ,
,
∴sinB=![]() =
=![]() =
=![]() ,
,
∴∠B=60°,
∴∠BOD=60°,
∴S扇形BOD=![]() =6π.
=6π.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目