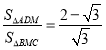题目内容
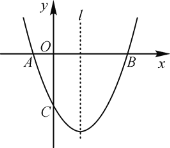
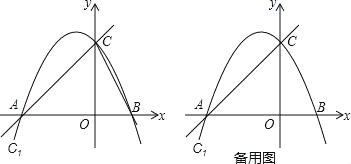
【题目】如图,抛物线![]() 与x轴交于A(﹣4,0)、B(2,0)两点,与y轴交于C,M为此抛物线的顶点.
与x轴交于A(﹣4,0)、B(2,0)两点,与y轴交于C,M为此抛物线的顶点.
(1)求此抛物线的函数解析式;
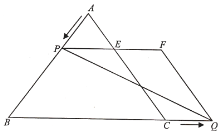
(2)动直线l从与直线AC重合的位置出发,绕点A顺时针旋转,与直线AB重合时终止运动,直线l与BC交于点D,P是线段AD的中点.
①直接写出点P所经过的路线长为 ;
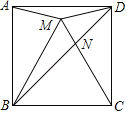
②点D与B、C不重合时,过点D作DE⊥AC于点E,作DF⊥AB于点F,连接PE、PF、EF,在旋转过程中,求EF的最小值;
(3)将抛物线C1平移得到抛物线C2,已知抛物线C2的顶点为N,与直线AC交于E、F两点,若EF=AC,求直线MN的解析式.
【答案】(1)y=﹣![]() x2﹣x+4;(2)①
x2﹣x+4;(2)①![]() ;②
;②![]() ;(3)y=x+
;(3)y=x+![]()
【解析】
(1)将点A、点B的坐标代入抛物线的解析式即可解决问题;
(2)①易得点P运动的路径是△ABC的中位线P1P2,只需运用勾股定理求出BC长,然后运用三角形中位线定理就可解决问题;②根据直角三角形斜边上的中线等于斜边的一半可得PE=PA=PD=PF,由此可得点A、E、D、F在以点P为圆心,![]() 为半径的圆上,根据圆周角定理可得∠EPF=2∠EAF.易得∠EAF=45°,则有∠EPF=90°,根据勾股定理可得
为半径的圆上,根据圆周角定理可得∠EPF=2∠EAF.易得∠EAF=45°,则有∠EPF=90°,根据勾股定理可得![]() ,根据“点到直线之间垂线段最短”可得当AD⊥BC时,AD最小,此时EF最小,然后只需运用面积法求出此时AD的值,即可得到EF的最小值;
,根据“点到直线之间垂线段最短”可得当AD⊥BC时,AD最小,此时EF最小,然后只需运用面积法求出此时AD的值,即可得到EF的最小值;
(3)运用待定系数法可求得直线AC的解析式为y=x+4,由EF=AC可得MN∥AC,从而可设直线MN的解析式为y=x+t,然后只需求出抛物线的顶点M的坐标,把点M的坐标代入y=x+t即可解决问题.
解:(1)∵抛物线![]() 与x轴交于A(﹣4,0)、B(2,0)两点,
与x轴交于A(﹣4,0)、B(2,0)两点,
∴![]() ,
,
解得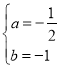 ,
,
∴抛物线的解析式为y=﹣![]() x2﹣x+4;
x2﹣x+4;
(2)①在Rt△BOC中,
![]() .
.
∵点D是线段BC一点,P是线段AD的中点,
∴点P运动的路径是△ABC的中位线P1P2,如图1,
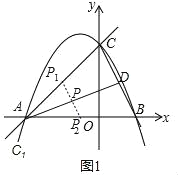
则![]() .
.
故答案为:![]() ;
;
②如图2,
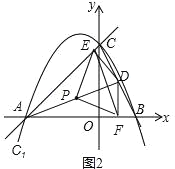
∵DE⊥AC,DF⊥AB,P是线段AD的中点,
∴PE=PA=PD=PF,
∴点A、E、D、F在以点P为圆心,![]() 为半径的圆上,
为半径的圆上,
∴∠EPF=2∠EAF.
∵OA=OC=4,∠AOC=90°,
∴∠CAO=∠ACO=45°,
∴∠EPF=90°,
∴![]() .
.
根据“点到直线之间,垂线段最短”可得:
当AD⊥BC时,AD最小,此时EF最小,
此时,![]() ,
,
解得:![]() ,
,
此时![]() ,
,
则EF的最小值为![]() ;
;
(3)如图3,
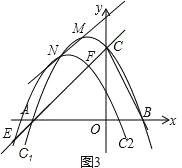
设直线AC的解析式为y=mx+n,
则有![]() ,
,
解得:![]() ,
,
∴直线AC的解析式为y=x+4.
由EF=AC可得MN∥AC.
可设直线MN的解析式为y=x+t.
∵点M是抛物线![]() 的顶点,
的顶点,
∴点M的坐标为(﹣1,![]() ),
),
把M(﹣1,![]() )代入y=x+t,得
)代入y=x+t,得
﹣1+t=![]() ,
,
解得t=![]() ,
,
∴直线MN的解析式为y=x+![]() .
.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案