Question

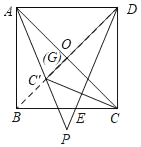
【题目】如图，在正方形ABCD中，E是边BC上的一动点（不与点B、C重合），连接DE、点C关于直线DE的对称点为C′，连接AC′并延长交直线DE于点P，F是AC′的中点，连接DF．

（1）求∠FDP的度数；

（2）连接BP，请用等式表示AP、BP、DP三条线段之间的数量关系，并证明；

（3）连接AC，若正方形的边长为，请直接写出△ACC′的面积最大值．

Answer 1

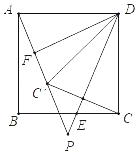
【答案】（1）45°；（2）BP+DP＝AP，证明详见解析；（3）﹣1．

【解析】

（1）证明∠CDE＝∠C'DE和∠ADF＝∠C'DF，可得∠FDP'＝∠ADC＝45°；

（2）作辅助线，构建全等三角形，证明△BAP≌△DAP'（SAS），得BP＝DP'，从而得△PAP'是等腰直角三角形，可得结论；

（3）先作高线C'G，确定△ACC′的面积中底边AC为定值2，根据高的大小确定面积的大小，当C'在BD上时，C'G最大，其△ACC′的面积最大，并求此时的面积．

（1）由对称得：CD＝C'D，∠CDE＝∠C'DE，

在正方形ABCD中，AD＝CD，∠ADC＝90°，

∴AD＝C'D，

∵F是AC'的中点，

∴DF⊥AC'，∠ADF＝∠C'DF，

∴∠FDP＝∠FDC'+∠EDC'＝∠ADC＝45°；

（2）结论：BP+DP＝AP，

理由是：如图，作AP'⊥AP交PD的延长线于P'，

∴∠PAP'＝90°，

在正方形ABCD中，DA＝BA，∠BAD＝90°，

∴∠DAP'＝∠BAP，

由（1）可知：∠FDP＝45°

∵∠DFP＝90°

∴∠APD＝45°，

∴∠P'＝45°，

∴AP＝AP'，

在△BAP和△DAP'中，

∵，

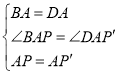∴△BAP≌△DAP'（SAS），

∴BP＝DP'，

∴DP+BP＝PP'＝AP；

（3）如图，过C'作C'G⊥AC于G，则S△AC'C＝ACC'G，

Rt△ABC中，AB＝BC＝，

∴AC＝，即AC为定值，

当C'G最大值，△AC'C的面积最大，

连接BD，交AC于O，当C'在BD上时，C'G最大，此时G与O重合，

∵CD＝C'D＝，OD＝AC＝1，

∴C'G＝﹣1，

∴S△AC'C＝．