题目内容
【题目】如图1所示,点E在弦AB所对的优弧上,且![]() 为半圆,C是
为半圆,C是![]() 上的动点,连接CA、CB,已知AB=4cm,设B、C间的距离为xcm,点C到弦AB所在直线的距离为y1cm,A、C两点间的距离为y2cm.
上的动点,连接CA、CB,已知AB=4cm,设B、C间的距离为xcm,点C到弦AB所在直线的距离为y1cm,A、C两点间的距离为y2cm.
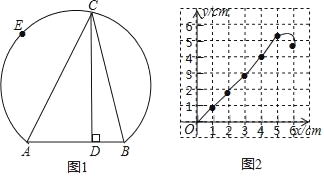
小明根据学习函数的经验,分别对函数y1、y2岁自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整.
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1、y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 0.78 | 1.76 | 2.85 | 3.98 | 4.95 | 4.47 |
y2/cm | 4 | 4.69 | 5.26 | 5.96 | 5.94 | 4.47 |
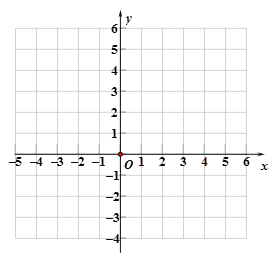
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1、y2的图象;
(3)结合函数图象,解决问题:
①连接BE,则BE的长约为 cm.
②当以A、B、C为顶点组成的三角形是直角三角形时,BC的长度约为 cm.
【答案】(1)详见解析;(2)详见解析;(3)①6;②6或4.47.
【解析】
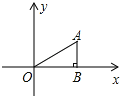
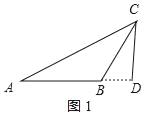
(1)由题意得出BC=3cm时,CD=2.85cm,从点C与点B重合开始,一直到BC=4,CD、AC随着BC的增大而增大,则CD一直与AB的延长线相交,由勾股定理得出BD=![]() ,得出AD=AB+BD=4.9367(cm),再由勾股定理求出AC即可;
,得出AD=AB+BD=4.9367(cm),再由勾股定理求出AC即可;
(2)描出补全后的表中各组数值所对应的点(x,y1),(x,y2),画出函数y1、y2的图象即可;
(3)①∵BC=6时,CD=AC=4.47,即点C与点E重合,CD与AC重合,BC为直径,得出BE=BC=6即可;
②分两种情况:当∠CAB=90°时,AC=CD,即图象y1与y2的交点,由图象可得:BC=6;
当∠CBA=90°时,BC=AD,由圆的对称性与∠CAB=90°时对称,AC=6,由图象可得:BC=4.47.
(1)由表中自变量x的值进行取点、画图、测量,分别得到了y1、y2与x的几组对应值知:BC=3cm时,CD=2.85cm,从点C与点B重合开始,一直到BC=4,CD、AC随着BC的增大而增大,则CD一直与AB的延长线相交,如图1所示:
∵CD⊥AB,
∴![]() (cm),
(cm),
∴AD=AB+BD=4+0.9367=4.9367(cm),
∴![]() (cm);
(cm);
补充完整如下表:

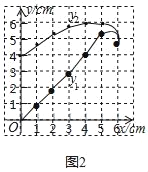
(2)描出补全后的表中各组数值所对应的点(x,y1),(x,y2),画出函数y1、y2的图象如图2所示:
(3)①∵BC=6cm时,CD=AC=4.47cm,即点C与点E重合,CD与AC重合,BC为直径,
∴BE=BC=6cm,
故答案为:6;
②以A、B、C为顶点组成的三角形是直角三角形时,分两种情况:
当∠CAB=90°时,AC=CD,即图象y1与y2的交点,由图象可得:BC=6cm;
当∠CBA=90°时,BC=AD,由圆的对称性与∠CAB=90°时对称,AC=6cm,由图象可得:BC=4.47cm;
综上所述:BC的长度约为6cm或4.47cm;
故答案为:6或4.47.

 阅读快车系列答案
阅读快车系列答案【题目】某中学开展“头脑风暴”知识竞赛活动,八年级![]() 班和
班和![]() 班各选出
班各选出![]() 名选手参加初赛,两个班的选手的初赛成绩(单位:分)分别是:
名选手参加初赛,两个班的选手的初赛成绩(单位:分)分别是:
1班85 80 75 85 100
2班80 100 85 80 80
(1)根据所给信息将下面的表格补充完整;
平均数 | 中位数 | 众数 | 方差 | |
|
|
| ||
|
|
|
(2)根据问题(1)中的数据,判断哪个班的初赛成绩较为稳定,并说明理由.