题目内容
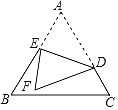
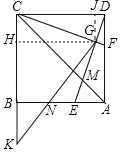
【题目】 如图,正方形ABCD的边长为6,点E,点F分别在边AB,AD上,AE=DF=2,连接DE,CF交于点G.连接AC与DE交于点M,延长CB至点K,使BK=3,连接GK交AB于点N.
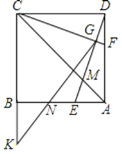
(1)求证:CF⊥DE;
(2)求△AMD的面积;
(3)请直接写出线段GN的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)证明△CDF≌△DAE(SAS),推出∠DCF=∠ADE可得结论.
(2)由AE∥CD,推出![]() ,推出DM=
,推出DM=![]() DE,推出S△ADM=
DE,推出S△ADM=![]() S△ADE可得结论.
S△ADE可得结论.
(3)过点G作GJ⊥CD于J,GH⊥BC于H.解直角三角形求出HK,HG,再利用勾股定理求解即可.
(1)证明:∵四边形ABCD是正方形,
∴CD=AD,∠CDF=∠DAE=90°,
∵DF=AE,
∴△CDF≌△DAE(SAS),
∴∠DCF=∠ADE,
∵∠ADE+∠CDE=90°,
∴∠DCF+∠ADE=90°,
∴∠CGD=90°,
∴CF⊥DE.
(2)解:∵AE∥CD,
∴![]() ,
,
∴DM=![]() DE,
DE,
∴S△ADM=![]() S△ADE=
S△ADE=![]() ×
×![]() ×2×6=4.
×2×6=4.
(3)解:过点G作GJ⊥CD于J,GH⊥BC于H.
∵DG⊥CF,
∴DG=![]() ,
,
∴CG=![]() =
=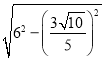 =
=![]() ,
,
∵GJ⊥CD,
∴GJ=CH=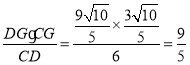 ,
,
∴GH=CJ=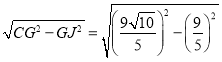 =
=![]() ,HK=6﹣
,HK=6﹣![]() +3=
+3=![]()
∴GK=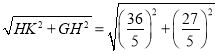 =9.
=9.

练习册系列答案
相关题目