题目内容
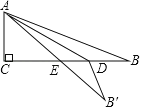
【题目】如图,在Rt△ABC的纸片中,∠C=90°,AC=5,AB=13.点D在边BC上,以AD为折痕将△ADB折叠得到△ADB′,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是___.
【答案】7或![]() .
.
【解析】
由勾股定理可以求出BC的长,由折叠可知对应边相等,对应角相等,当△DEB′为直角三角形时,可以分为两种情况进行考虑,分别利用勾股定理可求出BD的长.
在Rt△ABC中,![]() ,
,
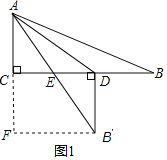
(1)当∠EDB′=90°时,如图1,
过点B′作B′F⊥AC,交AC的延长线于点F,
由折叠得:AB=AB′=13,BD=B′D=CF,
设BD=x,则B′D=CF=x,B′F=CD=12﹣x,
在Rt△AFB′中,由勾股定理得:
![]() ,
,
即:x2﹣7x=0,解得:x1=0(舍去),x2=7,
因此,BD=7.
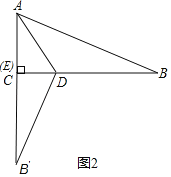
(2)当∠DEB′=90°时,如图2,此时点E与点C重合,
由折叠得:AB=AB′=13,则B′C=13﹣5=8,
设BD=x,则B′D=x,CD=12﹣x,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,解得:
,解得:![]() ,
,
因此![]() .
.
故答案为:7或![]() .
.

练习册系列答案
相关题目