题目内容
【题目】如图，抛物线
经过
，
两点，与y轴交于点C，连接AB，AC，BC．
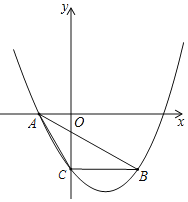
求抛物线的表达式；
求证：AB平分
；
抛物线的对称轴上是否存在点M，使得
是以AB为直角边的直角三角形，若存在，求出点M的坐标；若不存在，请说明理由．
【答案】
抛物线的解析式为
；
证明见解析；
点M的坐标为
或
．
【解析】
将
，
代入抛物线的解析式得到关于a、b的方程组，从而可求得a、b的值；
先求得AC的长，然后取
，则
，连接BD，接下来，证明
，然后依据SSS可证明
≌
，接下来，依据全等三角形的性质可得到
；
作抛物线的对称轴交x轴与点E，交BC与点F，作点A作
，作
，分别交抛物线的对称轴与
、M，依据点A和点B的坐标可得到
，从而可得到
或
，从而可得到FM和
的长，故此可得到点和点M的坐标．
将，代入得：
，
解得：
，
，
抛物线的解析式为；
，
，
，
取，则
，
由两点间的距离公式可知
，
，，
，
，
在和中，，
，
，
≌，
，
平分
；
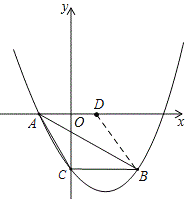
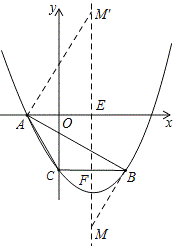
如图所示：抛物线的对称轴交x轴与点E，交BC与点F．
抛物线的对称轴为
，则
．
，，
，
，
，
，
，
同理：
，
又
，
，
，
点M的坐标为或．
练习册系列答案
百年学典课时学练测系列答案
相关题目
