Question

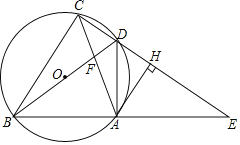
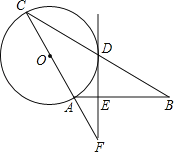
【题目】如图，在△ABC中，AB＝AC，以AC为直径做⊙O交BC于点D，过点D作⊙O的切线，交AB于点E，交CA的延长线于点F．

（1）求证：FE⊥AB；

（2）填空：当EF＝4，时，则DE的长为　 　．

Answer 1

【答案】（1）详见解析；（2）6.

【解析】

(1)连接OD，如图，先根据切线的性质得到OD⊥DF，然后利用等腰三角形的性质和平行线的判定证明OD∥AB，从而可判断EF⊥AB；

(2)根据平行线分线段比例，由AE∥OD得，然后根据比例性质可求出DE．

(1)连接OD，如图，

∵DF为⊙O的切线，

∴OD⊥DF，

∵OC＝OD，

∴∠C＝∠ODC，

∵AB＝AC，

∴∠B＝∠C，

∴∠B＝∠ODC，

∴OD∥AB，

∴EF⊥AB；

(2)∵AE∥OD，

∴，

即，解得DE＝6，

故答案为：6．