Question

【题目】如图，在平面直角坐标系xOy中，矩形AOCD的顶点A的坐标是（0，4），现有两动点P，Q，点P从点O出发沿线段OC（不包括端点O，C）以每秒2个单位长度的速度匀速向点C运动，点Q从点C出发沿线段CD（不包括端点C，D）以每秒1个单位长度的速度匀速向点D运动．点P，Q同时出发，同时停止，设运动时间为t（秒），当t=2（秒）时，PQ=2 ．
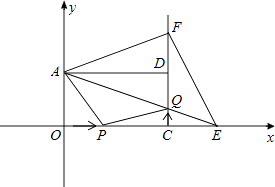
（1）求点D的坐标，并直接写出t的取值范围．
（2）连接AQ并延长交x轴于点E，把AE沿AD翻折交CD延长线于点F，连接EF，则△AEF的面积S是否随t的变化而变化？若变化，求出S与t的函数关系式；若不变化，求出S的值．
（3）在（2）的条件下，t为何值时，四边形APQF是梯形？

Answer 1

【答案】
（1）解：由题意可知，当t=2（秒）时，OP=4，CQ=2，

在Rt△PCQ中，由勾股定理得：PC= =4，

∴OC=OP+PC=4+4=8，

又∵矩形AOCD，A（0，4），∴D（8，4）．

点P到达终点所需时间为 =4秒，点Q到达终点所需时间为 =4秒，由题意可知，t的取值范围为：0＜t＜4．

（2）解：结论：△AEF的面积S不变化．

∵AOCD是矩形，∴AD∥OE，∴△AQD∽△EQC，

∴ ，即 ，解得CE= ．

由翻折变换的性质可知：DF=DQ=4﹣t，则CF=CD+DF=8﹣t．

S=S梯形AOCF+S△FCE﹣S△AOE

= （OA+CF）OC+ CFCE﹣ OAOE

= [4+（8﹣t）]×8+ （8﹣t） ﹣ ×4×（8+ ）

化简得：S=32为定值．

所以△AEF的面积S不变化，S=32．

（3）解：若四边形APQF是梯形，因为AP与CF不平行，所以只有PQ∥AF．

由PQ∥AF可得：△CPQ∽△DAF，

∴ ，即 ，化简得t2﹣12t+16=0，

解得：t1=6+2 ，t2=6﹣2 ，

由（1）可知，0＜t＜4，∴t1=6+2 不符合题意，舍去．

∴当t=（6﹣2 ）秒时，四边形APQF是梯形．

【解析】（1）利用勾股定理求出PC的长度，然后利用矩形的性质确定D点的坐标；自变量的取值范围由动点到达终点的时间来确定；（2）本问关键是利用相似三角形与翻折变换的性质，求出S的表达式．注意求图形面积的方法S=S梯形AOCF+S△FCE﹣S△AOE ． 经化简计算后，S=32为定值，所以S不变；（3）由四边形APQF是梯形，可得PQ∥AF，从而得到相似三角形△CPQ∽△DAF；再由线段比例关系求出时间t．
【考点精析】关于本题考查的梯形的定义和翻折变换（折叠问题），需要了解一组对边平行，另一组对边不平行的四边形是梯形．两腰相等的梯形是等腰梯形；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能得出正确答案．