Question

【题目】如图，在长方形ABCD中，AB：BC=3：4，AC=5，点P从点A出发，以每秒1个单位的速度，沿△ABC边A→B→C→A的方向运动，运动时间为t秒．

（1）求AB与BC的长；

（2）在点P的运动过程中，是否存在这样的点P，使△CDP为等腰三角形？若存在，求出t值；若不存在，说明理由．

Answer 1

【答案】（1）AB=3，BC=4；（2）存在；9.5秒或10秒或1.5秒或4秒或10.6秒.

【解析】

（1）利用因式分解法解出方程即可；

（2）分PC=CD、PD=PC、PD=CD三种情况，根据等腰三角形的性质和勾股定理计算即可．

解：（1）设AB=3x，BC=4x

在Rt△ABC中，AB2+BC2=AC2，

∴AC=5x，5x=5，x=1

∴AB=3，BC=4，

（2）存在点P，使△CDP是等腰三角形，理由如下：

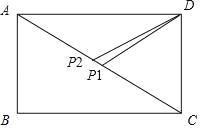
当P1D=P1C即P为对角线AC中点时，△CDP是等腰三角形，

∵AB=3，BC=4，

∴，

∴，

∴（秒）

当CD=P2C时，△CDP是等腰三角形，

∴（秒），

AB的中点也是，此时t=1.5；

CP=CD，P在BC线段上，此时，t=4；

DP=DC，P在线段AC上，此时t=10.6；

综上可知当t=9.5秒或10秒或1.5秒或4秒或10.6秒时△CDP是等腰三角形．