ЬтФПФкШн
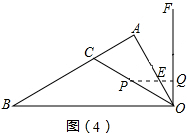
ШчЭМЃЈ1ЃЉЃЌдкRtЁїAOBжаЃЌЁЯA=90ЁуЃЌAB=6ЃЌOB=4
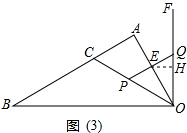
ЃЌЁЯAOBЕФЦНЗжЯпOCНЛABгкCЃЌЙ§OЕузїгыOBДЙжБЕФжБЯпOFЃЎЖЏЕуPДгЕуBГіЗЂбиелЯпBCЁњCOЗНЯђвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуOдЫЖЏЃЌЭЌЪБЖЏЕуQДгЕуCГіЗЂбиелCOЁњOFЗНЯђвдЯрЭЌЕФЫйЖШдЫЖЏЃЌЩшЕуPЕФдЫЖЏЪБМфЮЊtУыЃЌЕБЕуPЕНДяЕуOЪБPЁЂQЭЌЪБЭЃжЙдЫЖЏЃЎ
ЃЈ1ЃЉЧѓOCЁЂBCЕФГЄЃЛ
ЃЈ2ЃЉЩшЁїCPQЕФУцЛ§ЮЊSЃЌЧѓSгыtЕФКЏЪ§ЙиЯЕЪНЃЛ
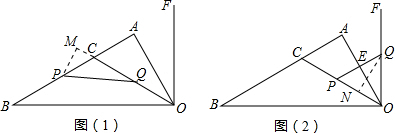
ЃЈ3ЃЉЕБЕуPдкOCЩЯЁЂЕуQдкOFЩЯдЫЖЏЪБЃЌШчЭМЃЈ2ЃЉЃЌPQгыOAНЛгкЕуEЃЌЕБtЮЊКЮжЕЪБЃЌЁїOPEЮЊЕШбќШ§НЧаЮЃПЧѓГіЫљгаТњзуЬѕМўЕФtЕФжЕЃЎ

| 3 |
ЃЈ1ЃЉЧѓOCЁЂBCЕФГЄЃЛ
ЃЈ2ЃЉЩшЁїCPQЕФУцЛ§ЮЊSЃЌЧѓSгыtЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЕБЕуPдкOCЩЯЁЂЕуQдкOFЩЯдЫЖЏЪБЃЌШчЭМЃЈ2ЃЉЃЌPQгыOAНЛгкЕуEЃЌЕБtЮЊКЮжЕЪБЃЌЁїOPEЮЊЕШбќШ§НЧаЮЃПЧѓГіЫљгаТњзуЬѕМўЕФtЕФжЕЃЎ

ЃЈ1ЃЉдкRtЁїAOBжаЃЌЁЯA=90ЁуЃЌAB=6ЃЌOB=4
ЃЌ
sinЁЯAOB=
=
=
ЃЌдђЁЯAOB=60ЁуЃЎ
вђЮЊOCЦНЗжЁЯAOBЃЌЁрЁЯAOC=30ЁуЃЌOA=
OB=2
ЃЎ
дкRtЁїAOCжаЃЌЁЯA=90ЁуЃЌЁЯAOC=30ЁуЃЌAC=
=2ЃЌOC=2AC=4ЃЌ
ЫљвдBC=AB-AC=4ЃЎ
ЃЈ2ЃЉБОЬтЗжШ§жжЧщПіЃК
ЂйЕБЕуPдкBCЩЯЁЂЕуQдкOCЩЯдЫЖЏЪБЃЌЃЈ0ЃМtЃМ4ЃЉШчЭМЃЈ1ЃЉCP=4-tЃЌCQ=t
Й§ЕуPзїPMЁЭOCНЛOCЕФбгГЄЯпгкЕуMЃЎ
дкRtЁїCPMжаЃЌЁЯM=90ЁуЃЌЁЯMCP=60Ёу
ЁрCM=
PC=
(4-t)ЃЌPM=
CM=
(4-t)ЃЌ
ЁпSЁїCPQ=
QC•PMЃЌ
ЁрS=
ЁСt•
(4-t)=
t(4-t)ЃЎ
ЂкЕБt=4ЪБЃЌЕуPгыЕуCжиКЯЃЌЕуQгыЕуOжиКЯЃЌДЫЪБЃЌВЛФмЙЙГЩЁїCPQЃЛ
ЂлЕБЕуPдкOCЩЯЁЂЕуQдкOQЩЯдЫЖЏЪБМДЃЈ4ЃМtЁм8ЃЉЃЌ
ШчЭМЃЈ2ЃЉPC=t-4ЃЌOQ=t-4ЃЌ
Й§ЕуQзїQNЁЭOCНЛOCгкЕуNЃЌ
дкRtЁїOQNжаЃЌЁЯQNO=90ЁуЃЌЁЯQON=60ЁуЃЌON=
OQ=
(t-4)ЃЌQN=
ON=
(t-4)ЃЌ
ЫљвдS=
PC•QN=
ЁС(t-4)•
(t-4)=
(t-4)2ЃЌ
злЩЯЫљЪіS=
ЃЎ
ЃЈ3ЃЉЁїOPEЮЊЕШбќШ§НЧаЮЗжШ§жжЧщПіЃК
ЂйЕБOP=OEЪБЃЌOQ=t-4ЃЌOP=8-t
Й§ЕуEзїEHЁЭOQгкЕуHЃЌдђQH=EH=
OEЃЌOH=
OEЃЌ
ЁрOQ=HQ+OH=(
+
)OE=t-4ЃЎЁрOE=
=OP=8-tЃЌНтЕУЃКt=
ЃЌ
ЂкЕБEP=EOЪБЃЌШчЭМЃКЁїOPQЮЊ30ЁуЕФжБНЧШ§НЧаЮЃЌOQ=
OPЃЌ
(8-t)=t-4ЃЌt=
ЃЎ
ЂлЕБPE=POЪБЃЌPEЁЮOFЃЌPEВЛгыOFЯрНЛЃЌЙЪЩсШЅЃЎ
злЩЯЫљЪіЃЌЕБt=
КЭt=
ЪБЃЌЁїOPEЮЊЕШбќШ§НЧЃЎ
| 3 |
sinЁЯAOB=
| AB |
| OB |
| 6 | ||
4
|
| ||
| 2 |
вђЮЊOCЦНЗжЁЯAOBЃЌЁрЁЯAOC=30ЁуЃЌOA=
| 1 |
| 2 |
| 3 |
дкRtЁїAOCжаЃЌЁЯA=90ЁуЃЌЁЯAOC=30ЁуЃЌAC=
| OA | ||
|
ЫљвдBC=AB-AC=4ЃЎ
ЃЈ2ЃЉБОЬтЗжШ§жжЧщПіЃК
ЂйЕБЕуPдкBCЩЯЁЂЕуQдкOCЩЯдЫЖЏЪБЃЌЃЈ0ЃМtЃМ4ЃЉШчЭМЃЈ1ЃЉCP=4-tЃЌCQ=t
Й§ЕуPзїPMЁЭOCНЛOCЕФбгГЄЯпгкЕуMЃЎ
дкRtЁїCPMжаЃЌЁЯM=90ЁуЃЌЁЯMCP=60Ёу
ЁрCM=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
ЁпSЁїCPQ=
| 1 |
| 2 |
ЁрS=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
ЂкЕБt=4ЪБЃЌЕуPгыЕуCжиКЯЃЌЕуQгыЕуOжиКЯЃЌДЫЪБЃЌВЛФмЙЙГЩЁїCPQЃЛ
ЂлЕБЕуPдкOCЩЯЁЂЕуQдкOQЩЯдЫЖЏЪБМДЃЈ4ЃМtЁм8ЃЉЃЌ
ШчЭМЃЈ2ЃЉPC=t-4ЃЌOQ=t-4ЃЌ
Й§ЕуQзїQNЁЭOCНЛOCгкЕуNЃЌ
дкRtЁїOQNжаЃЌЁЯQNO=90ЁуЃЌЁЯQON=60ЁуЃЌON=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
ЫљвдS=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
злЩЯЫљЪіS=
|
ЃЈ3ЃЉЁїOPEЮЊЕШбќШ§НЧаЮЗжШ§жжЧщПіЃК
ЂйЕБOP=OEЪБЃЌOQ=t-4ЃЌOP=8-t
Й§ЕуEзїEHЁЭOQгкЕуHЃЌдђQH=EH=
| 1 |
| 2 |
| ||
| 2 |

ЁрOQ=HQ+OH=(
| 1 |
| 2 |
| ||
| 2 |
| 2(t-4) | ||
1+
|
12+4
| ||
| 3 |
ЂкЕБEP=EOЪБЃЌШчЭМЃКЁїOPQЮЊ30ЁуЕФжБНЧШ§НЧаЮЃЌOQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 16 |
| 3 |
ЂлЕБPE=POЪБЃЌPEЁЮOFЃЌPEВЛгыOFЯрНЛЃЌЙЪЩсШЅЃЎ
злЩЯЫљЪіЃЌЕБt=
12+4
| ||
| 3 |
| 16 |
| 3 |



СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП

 Тњзу9a2-24ab+16b2=0ЃЌВЂга2a2b=2566ЃЌЁЯAЪЙЕУЗНГЬ
Тњзу9a2-24ab+16b2=0ЃЌВЂга2a2b=2566ЃЌЁЯAЪЙЕУЗНГЬ