题目内容
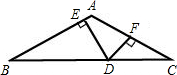
在△ABC中，AB=AC，D为BC上一点，由D分别作DE⊥AB于E，DF⊥AC于F．设DE=a，DF=b，且实数a，b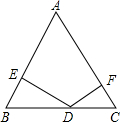
满足9a2-24ab+16b2=0，并有2a2b=2566，∠A使得方程
x2-x•sinA+
sinA-
=0有两个相等的实数根．
（1）试求实数a，b的值；
（2）试求线段BC的长．
满足9a2-24ab+16b2=0，并有2a2b=2566，∠A使得方程| 1 |
| 4 |
| 3 |
| 3 |
| 4 |
（1）试求实数a，b的值；
（2）试求线段BC的长．
（1）由条件有
，解得
；
（2）又由关于x的方程的判别式△=sin2A-
sinA+
=（sinA-
）2=0，则sinA=
，而∠A为三角形的一个内角，所以∠A1=60°或∠A2=120° 2分
当∠A=60°时，△ABC为正三角形，∠B=∠C=60°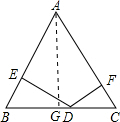
于是分别在Rt△BDE和Rt△CDF中
有BD=
=
，CD=
=2
所以BC=BD+DC=
．
当∠A=120°时，△ABC为等腰三角形，∠B=∠C=30°
同上方法可得BC=14． 3分
所以线段BC的长应为
或14．
|
|
（2）又由关于x的方程的判别式△=sin2A-
| 3 |
| 3 |
| 4 |
| ||
| 2 |
| ||
| 2 |
当∠A=60°时，△ABC为正三角形，∠B=∠C=60°
于是分别在Rt△BDE和Rt△CDF中
有BD=
| 4 |
| sin60° |
8
| ||
| 3 |
| 3 |
| sin60° |
| 3 |
所以BC=BD+DC=
| 14 |
| 3 |
| 3 |
当∠A=120°时，△ABC为等腰三角形，∠B=∠C=30°
同上方法可得BC=14． 3分
所以线段BC的长应为
14
| ||
| 3 |
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
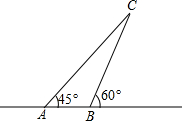
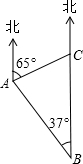
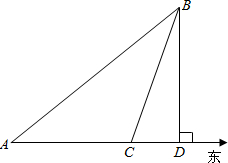行到C处，再测得海岛在东偏北60°，且船距海岛40海里．
