题目内容
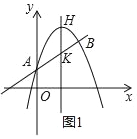
【题目】如图1，平面直角坐标系中，抛物线y=ax2﹣4ax+c与直线y=kx+1（k≠0）交于y轴上一点A和第一象限内一点B，该抛物线顶点H的纵坐标为5．
（1）求抛物线的解析式；
（2）连接AH、BH，抛物线的对称轴与直线y=kx+1（k≠0）交于点K，若S△AHB=
，求k的值；
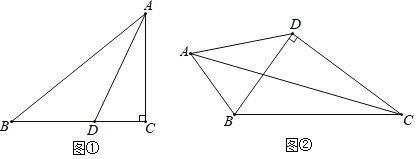
（3）在（2）的条件下，点P是直线AB上方的抛物线上的一动点（如图2），连接PA．当∠PAB=45°时，
ⅰ）求点P的坐标；
ⅱ）已知点M在抛物线上，点N在x轴上，当四边形PBMN为平行四边形时，请求出点M的坐标．
【答案】（1）y=﹣（x﹣2）2+5；（2）k=
；（3）ⅰ）P（1，4），ⅱ）M（﹣，﹣
）
【解析】
（1）抛物线
与直线
交于y轴上一点A，可求c=1，根据顶点纵坐标为5，可求
，即可求抛物线解析式．
（2）由
将线段的长代入可求k的值
（3）ⅰ）如图：将AB绕B点顺时针旋转90°到BC位置，过B点作BD⊥x轴，过点C点作CD⊥BD于D，过A点作AE⊥BD于E，可证△ABE≌△BCD，可得C点坐标，即可求AC解析式，由点P是直线AC与抛物线的交点可求P点坐标．
ⅱ）四边形PBMN为平行四边形，可得
根据中点坐标公式可求M的横坐标，代入抛物线可求M的坐标．
（1）∵抛物线
与直线交于y轴上一点A
∴
即c=1
∵抛物线
∴顶点坐标为
，
∴
∴
∴抛物线解析式
（2）∵抛物线与直线相交
∴
∴
∴B点横坐标为
∵点B在第一象限
∴
即
∵
∴
解得：
（不合题意舍去）
（3）ⅰ）如图：将AB绕B点顺时针旋转90°到BC位置，过B点作BD⊥x轴，过点C点作CD⊥BD于D，过A点作AE⊥BD于E
∵
∴
∵
∴
∵旋转
∴
∴
且
∴
且
∴
≌
∴
∴
设AC解析式
∴
=
b+1
∴b=3
∴AC解析式
∵P是直线AC与抛物线的交点
∴
∴
∴
ⅱ）如图2：设PN与BM的交点为H
∵四边形PBMN为平行四边形
∴
∵P的横坐标为1，N的横坐标为2．
∴H的横坐标为
∵B的横坐标为
∴M的横坐标为
∴
∴
