题目内容
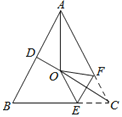
【题目】如图所示,CD为⊙O的直径,AD,AB,EC分别与⊙O相切于点D,E,C(AD<BC),连接DE并延长与与直线BC相交于点P,连接OB.
(1)求证:BC=BP;
(2)若DEOB=40,求ADBC的值;
(3)在(2)条件下,若S△ADE:S△PBE=16:25,求S△ADE和S△PBE.

【答案】(1)证明见解析;(2)20;(3)![]() .
.
【解析】
(1)连接EC,根据切线长定理可得BC=BE,再证得BE=BP,即可证得结论;(2)如图2中,连接OA、CE,EC交OB于K.先证明△OCK∽△OBC,可得OC2=OKOB=![]() DEOB=20,再证明△ADO∽△OCB,可得ADBC=ODOC=OC=20;(3)由△ADE∽△BPE,可得
DEOB=20,再证明△ADO∽△OCB,可得ADBC=ODOC=OC=20;(3)由△ADE∽△BPE,可得![]() ,设DE=4k,PE=5k,由△CDE∽△PDC,可得CD2=DEDP,即80=36k2,推出k=
,设DE=4k,PE=5k,由△CDE∽△PDC,可得CD2=DEDP,即80=36k2,推出k=![]() ,求出△PEC的面积即可解决问题.
,求出△PEC的面积即可解决问题.
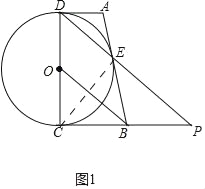
(1)证明:如图1中,连接EC.
∵BC、BE是⊙O的切线,
∴BC=BE,
∴∠BCE=∠BEC,
∵CD是直径,
∴∠CED=∠CEB=90°,
∴∠ECB+∠P=90°,∠CEB+∠CEB+∠PEB=90°,
∴∠P=∠PEB,
∴BE=PB,
∴BC=BP.
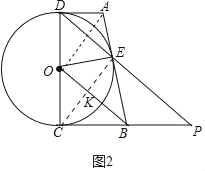
(2)解:如图2中,连接OA、CE,EC交OB于K.
∵BC=BE,OC=OE,
∴OB垂直平分线段EC,
∴∠OKC=∠OCB=90°,CK=EK,
∵OC=OD,
∴OK=![]() DE,
DE,
∵△OCK∽△OBC,
∴OC2=OKOB=![]() DEOB=20,
DEOB=20,
∵AD、AE是切线,
∴AD=AE,∵OD=OE,OA=OA,
∴△AOD≌△AOE,
∴∠AOD=∠AOE,同法证明,∠BOE=∠BOC,
∴∠AOB=90°,
∵∠AOD+∠BOC=90°,∠BOC+∠CBO=90°,
∴∠AOD=∠CBO,
∵∠ADO=∠BCO=90°,
∴△ADO∽△OCB,
∴ADBC=ODOC=OC2=20.
(3)如图2中,∵S△ADE:S△PBE=16:25,AD∥PB,
∴△ADE∽△BPE,
∴![]() =
=![]() ,设DE=4k,PE=5k,
,设DE=4k,PE=5k,
∵△CDE∽△PDC,
∴CD2=DEDP,
∴80=36k2,
∴k=![]() ,
,
∴DE=![]() ,PE=
,PE=![]() ,EC=
,EC=![]() ,
,
∴S△ECP=![]() ECPE=
ECPE=![]() ,∵BC=BP,
,∵BC=BP,
∴S△PEB=![]() S△PEC=
S△PEC=![]() ,
,
∴S△ADE=![]() S△PEB=
S△PEB=![]() .
.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】先填写表,通过观察后再回答问题:
a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| … | 0.01 | x | 1 | y | 100 | … |
(1)表格中x= ,y= ;
(2)从表格中探究a与![]() 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知![]() ≈3.16,则
≈3.16,则![]() ≈ ;
≈ ;
②已知![]() =8.973,若
=8.973,若![]() =897.3,用含m的代数式表示b,则b= ;
=897.3,用含m的代数式表示b,则b= ;
(3)试比较![]() 与a的大小.
与a的大小.
【题目】某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图,请根据图表信息回答下列问题:
初中毕业生视力抽样调查频数分布表
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)本次调查的样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?