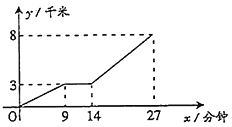
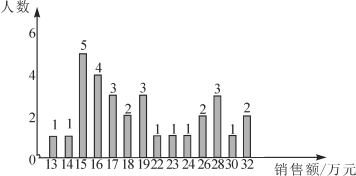
题目内容
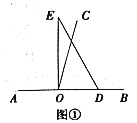
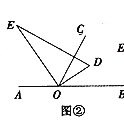
【题目】如图,将矩形纸片ABCD(图1)按如下步骤操作:
(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);
(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);
(3)将纸片收展平,那么∠AFE的度数为( )

A. 60° B. 67.5° C. 72° D. 75°
【答案】B
【解析】
折叠是一种对称变换,它属于轴对称,根据轴对称的性质,可利用角度的关系求解.
解:第一次折叠后,∠EAD=45°,∠AEC=135°;
第二次折叠后,∠AEF=67.5°,∠FAE=45°;
故由三角形内角和定理知,∠AFE=67.5度.
故选B.
本题考查图形的折叠变化及三角形的内角和定理.
关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.

练习册系列答案
相关题目