题目内容
【题目】如图所示, △ABC是直角三角形,∠A=90°,D是斜边BC的中点,E,F分别是AB,AC边上的动点,且DE⊥DF.

(1)如图(1),连接AD,若AB=AC=17,CF=5,求线段EF的长.
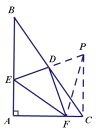
(2)如图(2),若AB≠AC,写出线段EF与线段BE,CF之间的等量关系,并写出证明过程.
【答案】(1)13;(2)EF2=BE2+CF2,证明过程见解析
【解析】
(1)由△ABC是等腰直角三角形,AD是斜边的中线,可得:∠DAC=∠BAD=∠C=45°,AD=DC,AD⊥BC,又DE⊥DF,根据同角的余角相等可得∠EDA=∠CDF,从而可证:△AED≌△CFD,所以可得AE=CF,然后由勾股定理可得出答案;
(2)延长ED到P,使DP=DE,连接FP,CP,利用SAS得到△BED≌△CPD,利用全等三角形的性质得到BE=CP,∠B=∠DCP,然后根据三线合一的性质得到EF=FP,然后求出∠FCP为直角,在直角三角形FCP中,利用勾股定理列出关系式,等量代换即可得证.
(1)∵在Rt△ABC中,AB=AC,AD为BC边的中线,
∴∠DAC=∠BAD=∠C=45°,AD⊥BC,AD=DC,
又∵DE⊥DF,AD⊥DC,
∴∠EDA+∠ADF=∠CDF+∠FDA=90°,
∴∠EDA=∠CDF,
在△AED与△CFD中,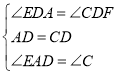 ,
,
∴△AED≌△CFD(ASA),
∴AE=CF,
∵AB=AC=17,CF=5,
∴AE=CF=5,AF=17-5=12,
在Rt△EAF中,由勾股定理得:![]() ;
;
(2)EF2=BE2+CF2;
如图,延长ED到P,使DP=DE,连接FP,CP,
在△BED和△CPD中,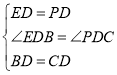 ,
,
∴△BED≌△CPD(SAS),
∴BE=CP,∠B=∠DCP,
∵DE⊥DF,DP=DE
∴EF=FP,
∵∠B=∠DCP,∠A=90°,
∴∠B+∠ACB=90°,
∴∠ACB+∠DCP=90°,即∠FCP=90°,
在Rt△FCP中,根据勾股定理得:CF2+CP2=PF2,
∵BE=CP,PF=EF,
∴EF2=BE2+CF2.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案【题目】某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图,请根据图表信息回答下列问题:
初中毕业生视力抽样调查频数分布表
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)本次调查的样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?









