题目内容
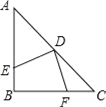
【题目】如图,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,求∠EDF的度数。

【答案】∠EDF=68°.
【解析】
由FD⊥BC,得∠FDC=90°;因∠AFD是△CDF的外角,∠AFD=158°,所以∠C=∠AFD∠FDC=158°90°=68°.由∠B=∠C,可得出∠B的度数.由DE⊥AB,得∠DEB=90°,进而求得∠BDE的度数,则∠EDF的度数即可求得.
∵FD⊥BC,所以∠FDC=90°,
∵∠AFD=∠C+∠FDC,
∴∠C=∠AFD﹣∠FDC=158°﹣90°=68°,
∴∠B=∠C=68°.
∵DE⊥AB,
∴∠DEB=90°,
∴∠BDE=90°﹣∠B=22°.
又∵∠BDE+∠EDF+∠FDC=180°,
∴∠EDF=180°﹣∠BDE﹣∠FDC=180°﹣22°﹣90°=68°.

练习册系列答案
相关题目
【题目】某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图,请根据图表信息回答下列问题:
初中毕业生视力抽样调查频数分布表
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)本次调查的样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?