题目内容
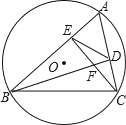
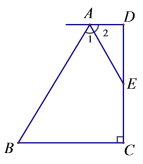
【题目】(本题满分9分)如图,以⊿ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且![]() .
.
(1)试判断⊿ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求![]() 的值.
的值.
【答案】(1)等腰三角形;(2)![]()
【解析】
试题分析:根据AB是直径,则我们很容易知道![]() ,同时也是
,同时也是![]() .进而就有
.进而就有
![]() ,而又
,而又![]() ,则DE=BE,进而
,则DE=BE,进而![]() ,所以
,所以![]() ,而ABED可以看成是个圆内接四边形,则
,而ABED可以看成是个圆内接四边形,则![]() ,所以
,所以![]() ,即⊿ABC为等腰三角形.
,即⊿ABC为等腰三角形.
第(2)问要求的是![]() 的正弦值,由图知,
的正弦值,由图知,![]() 在
在![]() 中,AB=10,要求正弦值,就必须求得AD的值,在
中,AB=10,要求正弦值,就必须求得AD的值,在![]() 中,我们可以利用等腰三角形一腰上的高求出AD=2.8,这样我们就能求出
中,我们可以利用等腰三角形一腰上的高求出AD=2.8,这样我们就能求出![]() .
.
试题解析:(1)∵AB为直径,
∴∠ADC=∠BDE=90°,∠C+∠DBC=90°,∠CDE+∠EDB=90°,
又∵![]() ,
,
∴∠EDB=∠DBC,
∴∠C=∠CDE,
∴CE=DE,
∵![]() ,
,
∴DE=BE,CE=BE,
∴AE垂直平分BC,
∴AC=BC,
∴△ABC为等腰三角形.
∵A,B,E,D四点共圆,
∴∠CDE=∠CBA,∠C公用,
∴△CDE∽△CBA,
∴![]()
∵BC=12,半径为5,
由(1)得AC=BC=10,CE=6,
即![]()
解得CD=7.2,
∴AD=AC-CD=2.8;
∴sin∠ABD=![]() =
=![]() .
.

练习册系列答案
相关题目