题目内容
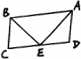
如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连结BE,且BE边平分∠ABC,则以下命题不正确的个数是
①BC+AD=AB;
②E为CD中点;
③∠AEB=90°;
④S△ABE=![]() S四边形ABCD;
S四边形ABCD;
⑤BC=CE
[ ]
A.0个
B.1个
C.2个
D.3个
答案:B
解析:
解析:
|
|

练习册系列答案
相关题目
题目内容
如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连结BE,且BE边平分∠ABC,则以下命题不正确的个数是

①BC+AD=AB;
②E为CD中点;
③∠AEB=90°;
④S△ABE=![]() S四边形ABCD;
S四边形ABCD;
⑤BC=CE
A.0个
B.1个
C.2个
D.3个
|
|
