��Ŀ����
����Ŀ����1����ֱ������ƽ���ڣ���֪��O�İ뾶ΪR����AΪ��O������һ�㣬����B��Բ��O�ľ���Ϊm���߶�AB�ij���Ϊl����m��Rʱ��l�����ֵ����Сֵ����Ϊ�� ������ ������m��Rʱ��l�����ֵ����Сֵ����Ϊ�� ������ ����
��2����ͼ����O�İ뾶Ϊ2����P�ġ�Kֵ���������£�����QΪ��O������һ�㣬�߶�PQ���ȵ����ֵ����Сֵ֮�Ϊ��P�ġ�Kֵ������ΪKP���ر�أ�����P��Q�غ�ʱ���߶�PQ�ij���Ϊ0��
������A��6��8����B����1��0������KA���� ����KB���� ����
����ֱ��y��2x��1�ϴ��ڵ�P��ʹ![]() �������P�ĺ����ꣻ
�������P�ĺ����ꣻ
��ֱ��![]() ��b��0����x�ᣬy��ֱ���A��B�����߶�AB�ϴ��ڵ�P��ʹ��
��b��0����x�ᣬy��ֱ���A��B�����߶�AB�ϴ��ڵ�P��ʹ��![]() ������ֱ��д��b��ȡֵ��Χ��
������ֱ��д��b��ȡֵ��Χ��
���𰸡���1��m+R��m��R��R+m��R��m����2����4��2����1��![]() ����1��b��2��
����1��b��2��
��������
��1����A��B��O��һ��ֱ����ʱ��AB��������Сֵ���ݴ˷ֱ���⼴�ɣ�
��2�����ȷֱ����AO��10��BO��1����KA����10+2������10��2����4��KB����2+1������2��1����2���ڵ���P��ԲO��ʱ��KP��2R��4�����������⣻����P��ԲO��ʱ��KP��2OP��2![]() ����P��m��2m��1��������m2+��2m��1��2��2��������m���۵�P����OΪԲ�ģ��뾶�ֱ�Ϊ
����P��m��2m��1��������m2+��2m��1��2��2��������m���۵�P����OΪԲ�ģ��뾶�ֱ�Ϊ![]() ��
��![]() Χ�ɵ�Բ���ڣ����߽磩�����߶�AB��ͼ����Ӱ�����й����㣬��
Χ�ɵ�Բ���ڣ����߽磩�����߶�AB��ͼ����Ӱ�����й����㣬��![]() ��b��0������OΪԲ�ģ�
��b��0������OΪԲ�ģ�![]() Ϊ�뾶��Բ����ʱ��
Ϊ�뾶��Բ����ʱ��![]() ��
��![]() �����b��1����
�����b��1����![]() ��b��0������OΪԲ�ģ�
��b��0������OΪԲ�ģ�![]() Ϊ�뾶��Բ����ʱ��
Ϊ�뾶��Բ����ʱ��![]() ��
��![]() �����b��2���Ӷ��ɵó�b��ȡֵ��Χ��
�����b��2���Ӷ��ɵó�b��ȡֵ��Χ��
�⣺��1����m��Rʱ����B��Բ�⣬
��ͼ2����A��B��O���㹲��ʱ��ABȡ�������Сֵ��
��A��Bλ��Բ��O����ʱABȡ�����ֵ�����ֵAB=BO+AO =m+R��
��A��Bλ��Բ��Oͬ��ʱABȡ����Сֵ����СֵAB=BO-AO=m��R��
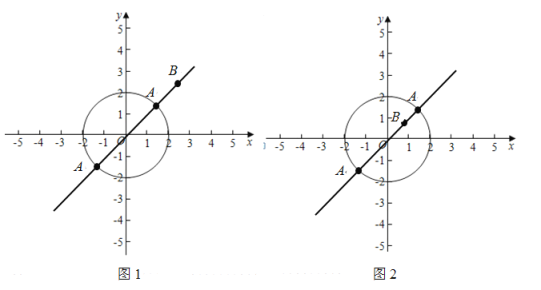
��m��Rʱ����B��Բ�ڣ���ͼ2��
ͬ���ɵã�AB�����ֵΪR+m����СΪR��m��
�ʴ�Ϊ��R+m��m��R��R+m��R��m��
��2�����ߵ�A��6��8����B����1��0����
��AO��10��BO��1��
��KA����10+2������10��2����4��
KB����2+1������2��1����2��
�ʴ�Ϊ4��2��
������P��ԲO��ʱ��KP��2R��4�����������⣻
����P��ԲO��ʱ��KP��2OP��2![]() ��
��
��OP��![]() ��
��
��P��ֱ��y��2x��1�ϣ�
��P��m��2m��1����
��m2+��2m��1��2��2��
��m��1��m����![]() ��
��
����P�ĺ�����Ϊ1��![]() ��
��
����![]() ��4��
��4��
���P��ԲO���ڲ���
����P����OΪԲ�ģ��뾶�ֱ�Ϊ![]() ��
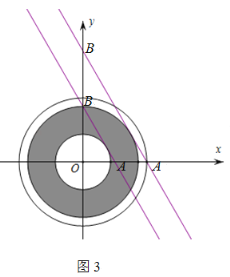
��![]() Χ�ɵ�Բ���ڣ����߽磩�����߶�AB��ͼ����Ӱ�����й����㣬��ͼ3��
Χ�ɵ�Բ���ڣ����߽磩�����߶�AB��ͼ����Ӱ�����й����㣬��ͼ3��
��![]() ��b��0������OΪԲ�ģ�
��b��0������OΪԲ�ģ�![]() Ϊ�뾶��Բ����ʱ��
Ϊ�뾶��Բ����ʱ��![]() ��
��![]() ����b��1��
����b��1��
��![]() ��b��0������OΪԲ�ģ�
��b��0������OΪԲ�ģ�![]() Ϊ�뾶��Բ����ʱ��
Ϊ�뾶��Բ����ʱ��![]() ��
��![]() ����b��2��
����b��2��
��b��ȡֵ��ΧΪ��1��b��2��