题目内容
如图,已知关于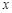 的一元二次函数
的一元二次函数 (
( )的图象与
)的图象与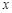 轴相交于
轴相交于 、
、 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴交于点
轴交于点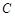 ,且
,且 ,顶点为
,顶点为 .
.
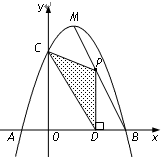
(1)求出一元二次函数的关系式;
(2)点 为线段
为线段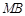 上的一个动点,过点
上的一个动点,过点 作
作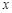 轴的垂线
轴的垂线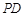 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为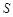 ,求
,求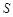 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(3)在(2)的条件下,当 点坐标是 时,
点坐标是 时, 为直角三角形.
为直角三角形.
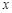 的一元二次函数
的一元二次函数 (
( )的图象与
)的图象与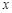 轴相交于
轴相交于 、
、 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴交于点
轴交于点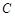 ,且
,且 ,顶点为
,顶点为 .
.
(1)求出一元二次函数的关系式;
(2)点
 为线段
为线段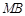 上的一个动点,过点
上的一个动点,过点 作
作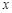 轴的垂线
轴的垂线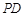 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为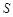 ,求
,求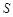 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;(3)在(2)的条件下,当
 点坐标是 时,
点坐标是 时, 为直角三角形.
为直角三角形.(1) ;(2)
;(2) (
(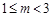 );
);
(3)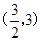 、
、
 ;(2)
;(2) (
(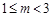 );
);(3)
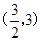 、
、
试题分析:(1)由
 可得
可得 、
、 ,即可根据待定系数法求解;
,即可根据待定系数法求解;(2)易得
 ,设
,设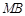 :
: ,根据待定系数法求得一次函数解析式,再根据三角形的面积公式求解即可;
,根据待定系数法求得一次函数解析式,再根据三角形的面积公式求解即可;(3)根据二次函数的性质及直角三角形的性质分类讨论即可.
(1)由
 可得
可得 、
、 .
.则
 得
得 ,
,所以
 ;
;(2)易得
 .
.设
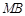 :
: ,
,则
 解得
解得
所以
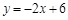 .
.所以
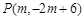 ,
, (
(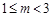 );
);(3)
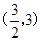 、
、 .
.点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
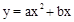 。
。 。
。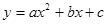 与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.M为y轴负半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N。
与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.M为y轴负半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N。
 ,求N点坐标;
,求N点坐标; 米。(1)若垂直于墙的一边长为
米。(1)若垂直于墙的一边长为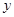 米,直接写出
米,直接写出


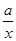 与正比例函数y=(b+c)x在同一坐标系中的大致图像可能是( )
与正比例函数y=(b+c)x在同一坐标系中的大致图像可能是( )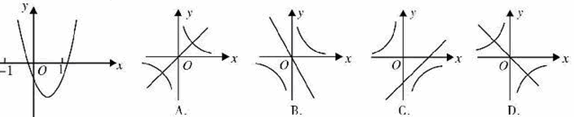
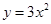 向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为 .
向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为 .