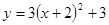题目内容
将抛物线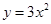 向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为 .
向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为 .
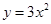 向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为 .
向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为 .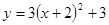
试题分析:抛物线
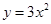 向上平移3个单位,那么得到新的抛物线为
向上平移3个单位,那么得到新的抛物线为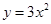 +3,在把抛物线为
+3,在把抛物线为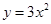 +3再向左平移2个单位,得到新的抛物线为
+3再向左平移2个单位,得到新的抛物线为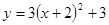
点评:本题考查抛物线的平移,解答本题的关键是掌握平移的概念,在平移的过程中向左、向右,向上、向下平移抛物线中的变量怎么变化

练习册系列答案
相关题目
题目内容
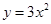 向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为 .
向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为 .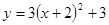
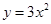 向上平移3个单位,那么得到新的抛物线为
向上平移3个单位,那么得到新的抛物线为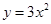 +3,在把抛物线为
+3,在把抛物线为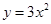 +3再向左平移2个单位,得到新的抛物线为
+3再向左平移2个单位,得到新的抛物线为