题目内容
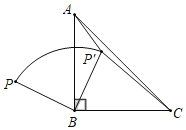
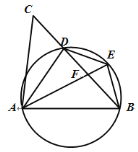
【题目】如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在圆上,连接AE,AE与BD相交于点F.
(1)求证:AE=AB;
(2)若E为弧BD的中点,试说明:DE2=EF·AE;
(3)在(2)的条件下,若cos∠ADB=![]() ,BE=2,求AF的长.
,BE=2,求AF的长.
【答案】(1)证明见解析;(2)证明见解析;(3) AF=3.
【解析】
(1)先根据翻折的性质和圆周角定理得出∠C=∠AED=∠ABC和AC=AE再推出AC=AB,从而得到AE=AB;
(2)根据E为弧BD的中点和圆周角定理得出∠DAE=∠EDB,然后证明△DEF∽△AED;
(3)作AH⊥BE,利用三角函数求出AE=4,利用(2)相似线段关系求出EF=1,从而得出:AF=3.
(1)由折叠的性质可知△ADE≌△ADC
∴∠AED=∠ACD,AE=AC,
∵∠ABD=∠AED,
∴∠ABD=∠ACD,
∴AB=AC,
∴AE=AB;
(2)∵E为弧BD的中点
∴∠DAE=∠EAB
∵∠EDB=∠EAB
∴∠DAE=∠EDB
∴△DEF∽△AED
∴![]()
∴![]()
(3)过A作AH⊥BE于点H

∵AB=AE,BE=2,
∴BH=EH=1,
∵∠ABE=∠AEB=∠ADB,![]() ,
,
∴![]() ,
,
∴![]() .
.
∴AC=AB=4
∵E为弧BD的中点
∴DE=EB=2
根据(2)中的结论![]()
可得:![]()
∴EF=1
∴AF=AE-EF=3

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目