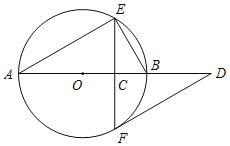
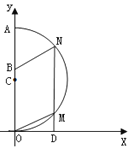
[题目]如图.在平面直角坐标系中.平行四边形BOMN的一边延长线交x轴于点D.OB=18.OD=12.点C为线段BO上一点.以C点为圆心.CO为半径的圆过M.N两点.且与y轴交于点A.则OA长为 . 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在平面直角坐标系中，平行四边形BOMN的一边延长线交x轴于点D，OB=18，OD=12，点C为线段BO上一点，以C点为圆心，CO为半径的圆过M、N两点，且与y轴交于点A，则OA长为_____.

【答案】30

【解析】

过点C做CE⊥MN，垂足为E，连接CM，根据平行四边形的性质得出MN=BO=18，再根据垂径定理得出EM的长，再证的四边形ODEC为矩形，就可得出CE=OD=12，再根据勾股定理得出CM的长，最后即可求解OA的长.

过点C做CE⊥MN，垂足为E，连接CM，如图所示：

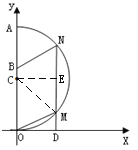
∵平行四边形BOMN

∴MN=OB=18

∵CE⊥MN，且C是圆心

∴CE垂直平分MN

∴

∵平行四边形BOMN的一边延长线交x轴于点D

∴

∴四边形是矩形

∴

故填：30.

练习册系列答案

（1）未降价之前，某商场衬衫的总盈利为　　元．

（2）降价后，设某商场每件衬衫应降价x元，则每件衬衫盈利　　元，平均每天可售出　　件（用含x的代数式进行表示）

（3）请列出方程，求出x的值．

【题目】如图，AB是⊙O的直径，弦EF⊥AB于点C，过点F作⊙O的切线交AB的延长线于点D．

（1）已知∠A＝α，求∠D的大小（用含α的式子表示）；

（2）取BE的中点M，连接MF，请补全图形；若∠A＝30°，MF＝，求⊙O的半径．

【题目】将正面分别写着数字1，2，3的三张卡片（注：这三张卡片的形状、大小、质地，颜色等其他方面完全相同，若背面上放在桌面上，这三张卡片看上去无任何差别）洗匀后，背面向上放在桌面上，从中先随机抽取一张卡片，记该卡片上的数字为x，再把剩下的两张卡片洗匀后，背面向上放在桌面上，再从这两张卡片中随机抽取一张卡片，记该卡片上的数字为y．

（1）用列表法或树状图法（树状图也称树形图）中的一种方法，写出（x，y）所有可能出现的结果．

（2）求取出的两张卡片上的数字之和为偶数的概率P．

【题目】已知关于的一元二次方程．

（1）若此方程的一个根为1，求的值；

（2）求证：不论取何实数，此方程都有两个不相等的实数根．

【题目】如图，D是△ABC的BC边上一点，连接AD，作△ABD的外接圆，将△ADC沿直线AD折叠，点C的对应点E落在圆上，连接AE，AE与BD相交于点F．

(1)求证：AE=AB；

(2)若E为弧BD的中点，试说明：DE2=EF·AE；

(3)在(2)的条件下，若cos∠ADB=，BE=2，求AF的长．

【题目】小华是数学兴趣小组的一名成员，他在学过二次函数的图像与性质之后，对的图像与性质进行了探究，探究过程如下，请你补充完整.

（1）小刚通过计算得到几组对应的数值如下

	…							0	1		2	3	4	5	…
	…		0	4	6		6	4	6		6	4	0		…

填空：自变量的取值范围是__________________，__________.

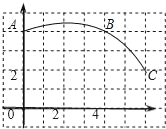
（2）在如图所示的平面直角坐标系中，描出上表中各组对应数值的点，并根据描出的点，画出该函数的图像.

（3）请你根据画出的图像，写出此函数的两条性质；

①__________________________________________；

②__________________________________________.

（4）直线经过，若关于的方程有4个不相等的实数根，则的取值范围为_________.

【题目】如图，矩形纸片，是的中点，是上一动点，沿折叠，点落在点处；延长交于点，连接.

（1）求证：≌；

（2）当时，将沿折叠，点落在线段上点处.

①求证：∽；

②如果，，求的长.

【题目】如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格中进行下列操作：

（1）请在图中确定该圆弧所在圆心D点的位置，D点坐标为　　；

（2）连接AD、CD，则⊙D的半径为　　；扇形DAC的圆心角度数为　　；

（3）若扇形DAC是某一个圆锥的侧面展开图，求该圆锥的底面半径．

试题分类