题目内容
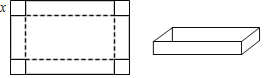
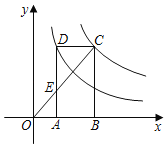
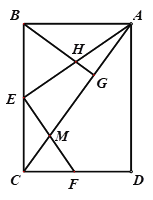
【题目】 如图,![]() 是矩形
是矩形![]() 的边
的边![]() 上的一点,AC是其对角线,连接AE,过点E作
上的一点,AC是其对角线,连接AE,过点E作![]() 交
交![]() 于点
于点![]() ,
, ![]() 交DC于点F,过点B作
交DC于点F,过点B作![]() 于点G,
于点G,![]() 交AE于点H.
交AE于点H.
(1)求证:![]() ∽
∽![]() ;
;
(2)求证:![]() ;
;
(3)若E是BC的中点,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)先利用等角的余角相等证明∠BAE=∠CEF,进一步即可证得结论;
(2)先利用等角的余角相等证明∠ABG=∠ACB,进而可证明△ABH∽△ECM,再利用相似三角形的性质即可证得结论;
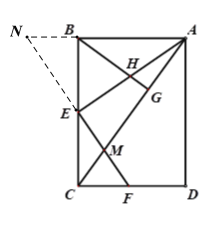
(3)由(1)利用相似三角形的性质可求出CF的长,进而利用勾股定理可求出EF的长,延长FE交AB的延长线于点N,易证△NBE≌△FCE,于是NB=FC,NE=FE,由CF∥AN可得△CMF∽△AMN,然后利用相似三角形的性质可求出FM的长,进一步即可求出结果.
解:(1)证明:∵四边形ABCD是矩形,
∴∠ABC=∠BCD=90°,
∴∠BAE+∠AEB=90°,
∵![]() ,∴∠AEB+∠CEF=90°,
,∴∠AEB+∠CEF=90°,
∴∠BAE=∠CEF,
∴![]() ∽
∽![]() ;
;
(2)证明:∵![]() ,∴∠BAG+∠ABG=90°,
,∴∠BAG+∠ABG=90°,
又∵∠BAC+∠ACB=90°,∴∠ABG=∠ACB,
∵∠BAH=∠ECM,
∴△ABH∽△ECM,
∴![]() ,
,
即![]() ;
;
(3)∵![]() ,
,![]() ,∴BC=8,∵E是BC的中点,∴BE=CE=4,
,∴BC=8,∵E是BC的中点,∴BE=CE=4,
由(1)知![]() ∽
∽![]() ,则
,则![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
则在Rt△CEF中,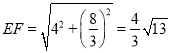 ,
,
延长FE交AB的延长线于点N,
∵∠NBE=∠FCE=90°,BE=CE,∠NEB=∠FEC,
∴△NBE≌△FCE,∴NB=FC,NE=FE,
∵CF∥AN,∴△CMF∽△AMN,∴ ,
,
∴![]() ,
,
∴![]() .
.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
|
| 0 | 2 | 3 | 4 |
| 5 | 0 |
|
| 0 |
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() ;④3是方程
;④3是方程![]() 的一个根;⑤若
的一个根;⑤若![]() ,
,![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中正确的个数是( )
,其中正确的个数是( )
A.1B.2C.3D.4