题目内容
【题目】如图,在![]() 中,
中,![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() ,
,![]() 的周长等于
的周长等于![]() 。
。
(1)求![]() 的长;
的长;
(2)若![]() ,并且
,并且![]() ,求证:
,求证:![]() 。
。

【答案】(1)10;(2)证明见详解
【解析】
(1)根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,然后求出△BCE的周长=AC+BC,再求解即可;
(2)根据等腰三角形两底角相等求出∠C=72°,根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,根据等边对等角可得∠ABE=∠A,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BEC=72°,从而得到∠BEC=∠C,然后根据等角对等边求解.
解:如图:
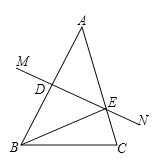
(1)∵AB的垂直平分线MN交AB于点D,:
∴AE=BE,
∴△BCE的周长=BE+CE+BC=AE+CE+BC=AC+BC,
∵AC=15cm,
∴BC=25-15=10cm;
(2)证明:∵∠A=36°,AB=AC,
∴∠C=![]() (180°-∠A)=
(180°-∠A)=![]() (180°-36°)=72°,
(180°-36°)=72°,
∵AB的垂直平分线MN交AB于点D,
∴AE=BE,
∴∠ABE=∠A,
由三角形的外角性质得,∠BEC=∠A+∠ABE=36°+36°=72°,
∴∠BEC=∠C,
∴BC=BE.

 阅读快车系列答案
阅读快车系列答案【题目】已知,在一个盒子旦有红球和白球共10个,它们除颜色外都相同,将它们充分摇匀后,从中随机抽出一个,记下颜色后放回.在摸球活动中得到如下数据:
摸球总次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
摸到红球的频率 | 17 | 32 | 44 | 64 | 78 | a | 103 | 122 | 136 | 148 |
摸到红球的频率 | 0.34 | 0.32 | 0.293 | 0.32 | 0.312 | 0.32 | 0.294 | b | 0.302 | c |
(1)请将表格中的数据补齐a= ;b= ;c= ;
(2)根据上表,完成折线统计图;

当摸球次数很大时,摸到红球的频率将会接近 (精确到0.1)
(3)请你估计,当摸球次数很大时,摸到红球的频率将会接近 (精确到0.1)